1.3 PROPERTIES OF ADDITION AND SUBTRACTION OF INTEGERS
NCERT Class 7 Mathematics Textbook for blind and visually impaired students made Screen Readable by Professor T K Bansal.
1.3.1 Closure under Addition
We have learnt that sum of two whole numbers is again a whole number. For example,
17 + 24 = 41 which is again a whole number.
We know that, this property is known as the closure property for addition of the whole numbers.
Let us see whether this property is true for integers or not.
Following are some pairs of integers. Observe the following table and complete it.
| Serial Number | Statement | Observation |
|---|---|---|
| (i) | 17 + 23 = 40 | Result is an integer |
| (ii) | (−10) + 3 = _____ | ______________ |
| (iii) | (−75) + 18 = _____ | ______________ |
| (iv) | 19 + (−25) = −6 | Result is an integer |
| (v) | 27 + (−27) = _____ | ______________ |
| (vi) | (−20) + 0 = _____ | ______________ |
| (vii) | (−35) + (−10) = _____ | ______________ |
What do you observe? Is the sum of two integers always an integer?
Did you find a pair of integers whose sum is not an integer?
Since addition of integers gives integers, we say integers are closed under addition.
In general, for any two integers a and b, a + b is an integer.
1.3.2 Closure under Subtraction
What happens when we subtract an integer from another integer? Can we say that their difference is also an integer?
Observe the following table and complete it:
| Serial Number | Statement | Observation |
|---|---|---|
| (i) | 7 − 9 = −2 | Result is an integer |
| (ii) | 17 − (−21) = _______ | ______________ |
| (iii) | (−8) − (−14) = 6 | Result is an integer |
| (iv) | (−21) − (− 10) = _______ | ______________ |
| (v) | 32 − (−17) = _______ | ______________ |
| (vi) | (−18) − (−18) = _______ | ______________ |
| (vii) | (−29) − 0 = _______ | ______________ |
What do you observe? Is there any pair of integers whose difference is not an integer?
Can we say integers are closed under subtraction? Yes, we can see that integers are closed under subtraction.
Thus, if a and b are two integers then a − b is also an integer.
Do the whole numbers satisfy this property?
1.3.3 Commutative Property
We know that 3 + 5 = 5 + 3 = 8, that is, the whole numbers can be added in any order. In other words, addition is commutative for whole numbers.
Can we say the same for integers also?
We have 5 + (− 6) = −1 and (− 6) + 5 = −1
So, 5 + (− 6) = (− 6) + 5
Are the following equal?
(i) (− 8) + (− 9) and (− 9) + (− 8)
(ii) (− 23) + 32 and 32 + (− 23)
(iii) (− 45) + 0 and 0 + (− 45)
Try this with five other pairs of integers.
Do you find any pair of integers for which the sums are different when the order is changed?
Certainly not.
We say that addition is commutative for integers.
In general, for any two integers a and b, we can say
a + b = b + a
• We know that subtraction is not commutative for whole numbers.
Is it commutative for integers?
Consider the integers 5 and (−3).
Is 5 − (−3) the same as (−3) −5?
No, because 5 − ( −3) = 5 + 3 = 8, and (−3) − 5
= − 3 − 5 = − 8.
Take at least five different pairs of integers and check this.
We conclude that subtraction is not commutative for integers.
1.3.4 Associative Property
Observe the following examples:
Consider the integers −3, −2 and −5.
Look at (−5) + [(−3) + (−2)] and [(−5) + (−3)] + (−2).
In the first sum (−3) and (−2) are grouped together and
in the second (−5) and (−3) are grouped together.
We will check whether we get different results.
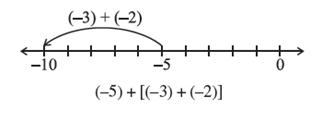
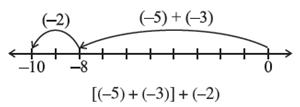
In both the cases, we get −10.
i.e., (−5) + [(−3) + (−2)] = [(−5) + (−2)] + (−3)
Similarly consider −3 , 1 and −7.
( −3) + [1 + (−7)] = −3 + __________ = __________
[(−3) + 1] + (−7) = −2 + __________ = __________
Is (−3) + [1 + (−7)] same as [(−3) + 1] + (−7)?
Take five more such examples. You will not find any example for which the sums are different. Addition is associative for integers.
In general for any integers a, b and c, we can say
a + (b + c) = (a + b) + c
1.3.5 Additive Identity
When we add zero to any whole number, we get the same whole number.
Zero is an additive identity for whole numbers.
Is it an additive identity again for integers also?
Observe the following and fill in the blanks:
(i) (− 8) + 0 = − 8
(ii) 0 + (− 8) = − 8
(iii) (−23) + 0 = _____
(iv) 0 + (−37) = −37
(v) 0 + (−59) = _____
(vi) 0 + _____ = − 43
(vii) − 61 + _____ = − 61
(viii) _____ + 0 = _____
The above examples show that zero is an additive identity for integers.
You can verify it by adding zero to any other five integers.
In general, for any integer a
a + 0 = a = 0 + a
TRY THESE 1.3
Q1. Write a pair of integers whose sum gives
(a) a negative integer
(b) zero
(c) an integer smaller than both the integers.
(d) an integer smaller than only one of the integers.
(e) an integer greater than both the integers.
Q2. Write a pair of integers whose difference gives
(a) a negative integer.
(b) zero.
(c) an integer smaller than both the integers.
(d) an integer greater than only one of the integers.
(e) an integer greater than both the integers.
EXAMPLE 1
Write down a pair of integers whose
(a) sum is −3
(b) difference is −5
(c) difference is 2
(d) sum is 0
SOLUTION:
(a) (−1) + (−2) = −3 or (−5) + 2 = −3
(b) (−9) − (− 4) = −5 or (−2) − 3 = −5
(c) (−7) − (−9) = 2 or 1 − (−1) = 2
(d) (−10) + 10 = 0 or 5 + (−5) = 0
Can you write more pairs in these examples?
EXERCISE 1.2
Q1. Write down a pair of integers whose:
(a) sum is −7
(b) difference is −10
(c) sum is 0
A1. One such pair could be:
(a) −10, 3
(b) − 6, 4; (− 6 − 4 = −10)
(c) −3, 3
Q2. (a) Write a pair of negative integers whose difference gives 8.
(b) Write a negative integer and a positive integer whose sum is −5.
(c) Write a negative integer and a positive integer whose difference is −3.
A2. One such pair could be:
(a) −2, −10; [−2 − (−10) = 8]
(b) − 6, 1
(c) −1, 2; (−1 − 2 = −3)
Q3. In a quiz, team A scored − 40, 10, 0 and team B scored 10, 0, − 40 in three successive rounds. Which team scored more? Can we say that we can add integers in any order?
A3. Scores of both the teams are same, i.e., −30; Yes
Q4. Fill in the blanks to make the following statements true:
(i) (−5) + (− 8) = (− 8) + (............)
(ii) −53 + ............ = −53
(iii) 17 + ............ = 0
(iv) [13 + (− 12)] + (............) = 13 + [(−12) + (−7)]
(v) (− 4) + [15 + (−3)] = [− 4 + 15] + ............
A4. (i) −5
(ii) 0
(iii) −17
(iv) −7
(v) −3
