NCERT Class 8 Mathematics Textbook for Blind and Visually Impaired Students made Screen Readable by Professor T K Bansal.

Can you tell the natural numbers between 1 and 5?
They are 2, 3 and 4.

How many natural numbers are there between 7 and 9?
There is only one, and it is 8.

How many natural numbers are there between 10 and 11?
Obviously none.

List the integers that lie between −5 and 4.
They are − 4, − 3, −2, −1, 0, 1, 2 and 3.

How many integers are there between −1 and 1?

How many integers are there between −9 and −10?

You will find that there are a definite number of natural numbers (or integers) between any two natural numbers (or integers).

How many rational numbers are there between 3/10 and 7/10?

You may have thought that there are only 3 numbers, namely, 4/10, 5/10 and 6/10.

But you can write these numbers also as
3/10 as 30/100;
and 7/10 as 70/100.

Now the numbers, 31/100, 32/100, 33/100, .. .. . , 68/100, 69/100, all lie between 3/10 and 7/10. The number of these rational numbers is 39.

Moreover, 3/10 can be expressed as 3000/10000, and 7/10 as 7000/10000 also
Now, we see that the rational numbers 3001/10000, 3002/10000, .. .., 6998/10000, 6999/10000, all lie between 3/10 and 7/10. These are 3999 numbers in all.

In this way, we can go on inserting more and more rational numbers between 3/10 and 7/10. So unlike natural numbers and integers, the number of rational numbers between any two rational numbers is not definite.

Here is one more example.

How many rational numbers are there between −1/10 and 3/10?
Obviously 0/10, 1/10, 2/10 are rational numbers between the given numbers.

If we write −1/10 as −10000/100000 and 3/10 as 30000/100000, we get the rational numbers −9999/100000, − 9998/100000, .. .., −29998/100000, 29999/100000, between −1/10 and 3/10.

You will find that you get countless rational numbers between any two given rational numbers.

Example 6

Write any 3 rational numbers between −2 and 0.

Solution:

−2 can be written as −20/10 and 0 as 0/10.
Thus we have −19/10, −18/10, −17/10, −16/10, −15/10, .. .. −1/10 between −2 and 0.
You can take any three of these.

Example 7

Find any ten rational numbers between −5/6 and 5/8.

Solution:

We first convert −5/6 and 5/8 to rational numbers with the same denominators.

First of all, let us find the LCM of 6 and 8, the denomenators of the two numbers, which is 24.

Now multiply the neumenator and denominator of − 5/6 by 4, and 5/8 by 3, to get,
(−5 × 4)/ (6 × 4) = −20/24 and
(5 × 3)/ (8 × 3) = 15/24

Thus we have −19/24, −18/24, −17/24 .. .. 14/24, as the rational numbers between −20/ 24 and 15/24.
You can take any ten of these.

Another Method to find more rational numbers between any two rational numbers:
Let us find rational numbers between 1 and 2.
One of them is 1.5 or 1 1/2 or 3/2.
This is the mean of 1 and 2.
You have studied mean in Class 7.

We find that between any two given numbers, we need not necessarily get an integer but there will always lie a rational number.

We can use the idea of mean also to find rational numbers between any two given rational numbers.

Example 8

Find a rational number between 1/4 and ½.

Solution:

We find the mean of the given rational numbers.
(1/4 + 1/2) ÷ 2
= ((1 + 2)/4) ÷ 2
= ¾ × ½ = 3/8

3/8 lies between ¼ and 1/2.

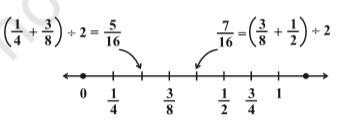
This can be seen on the number line also.

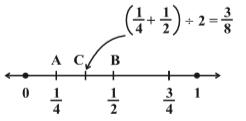
We find the midpoint of AB which is C, represented by (1/4 + ½) ÷ 2 = 3/8.
We find that ¼ < 3/8 < 1/2.

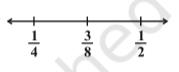
If a and b are two rational numbers, then (a + b)/2 is a rational number between a and b such that a < (a + b)/2 < b.

This again shows that there are countless number of rational numbers between any two given rational numbers.

Example 9

Find three rational numbers between 1/4 and 1/2.

Solution:

We find the mean of the given rational numbers.
As given in the previous example, the mean is 3/8 and
¼ < 3/8 < ½.

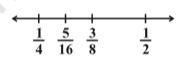
We now find another rational number between 1/4 and 3/8. For this, we again find the mean of
1/4 and 3/8.
That is, (1/4 + 3/8) ÷ 2
= 5/8 × ½ = 5/16
¼ < 5/16 < 3/8 < ½

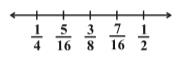
Now find the mean of 3/8 and 1/2.
We have, (3/8 + 1/2) ÷ 2
= 7/8 × ½ = 7/16

Thus we get ¼ < 5/16 < 3/8 < 7/16 < ½.
Thus, 5/16, 3/8, 7/16 are the three rational numbers between 1/4 and ½.
This can clearly be shown on the number line as follows:

In the same way we can obtain as many rational numbers as we want between any two given rational numbers .

You have noticed that there are countless rational numbers between any two given rational numbers.

EXERCISE 1.2

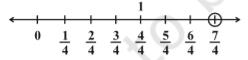
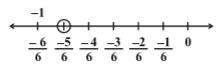
Q1. Represent these numbers on the number line.
(i) 7/4
(ii) −5/6

A1.
(i)

(ii)

Q2. Represent −2/11, −5/11, and −9/11 on the number line.

A2.

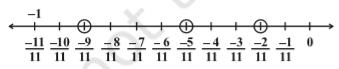
Q3. Write five rational numbers which are smaller than 2.

A3. Some of these are 1, ½, 0, −1, −1/2

Q4. Find ten rational numbers between −2/5 and ½.

A4. −7/20, −6/20, −5/20, −4/20, −3/20, −2/20, −1/20, 0 .. .., 1/20, 2/20
(There can be many more such rational numbers)

Q5. Find five rational numbers between.
(1) 2/3 and 4/5
(2) −3/2 and 5/3
(3) ¼ and ½

A5.
(1) 41/60, 42/60, 43/60, 44/60, 45/60, .. ..
(2) −8/6, −7/6, 0, 1/6, 2/6
(3) 9/32, 10/32, 11/32, 12/32, 13/32,
(There can be many more such rational numbers)

Q6. Write five rational numbers greater than −2.

A6. −3/2, −1, −1/2, 0, ½
(There can be many more such rational numbers)

Q7. Find ten rational numbers between 3/5 and ¾.

A7. 97/160, 98/160, 99/160, 100/160, 101/160, 102/160, 103/160, 104/160, 105/160, 106/160
(There can be many more such rational numbers)