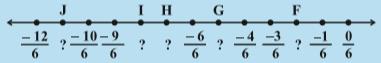1.3 Representation of Rational Numbers on the Number Line

Submitted by superadmin on 10 May, 2023 - 11:29

NCERT Class 8 Mathematics Textbook for Blind Students made Screen Readable by Professor T K Bansal.

You have learnt to represent natural numbers, whole numbers, integers and rational numbers on a number line. Let us revise them.

Natural numbers

Number line (1)

Figure shows a number line with marking at 1, 2, 3, 4, 5, 6, 7, & 8. It is mentioned that the line extends only to the right of 1. By Dr TKBansal.

Whole numbers

Number line (2)

Figure shows the number line extending till infinity to the right of 0. Whole numbers 0, 1, 2, 3, 4, 5, .. .. are marked on the number line. By Dr TKBansal.

Integers

Number line (3)

Figure shows a number line that extends on both sides of 0 till infinity. Numbers, -3, -2, -1, 0, 1, 2, 3, & 4 are marked on this number line . By Dr TKBansal.

Rational numbers

Number line (4)

Figure shows a numberline that extends on both sides of 0 indefinitely. However, you can now see numbers between -1, 0: 0, 1 etc. Numbers -1, -1/2, 0, 1/2, & 1 are marked on the numberline. By Dr TKBansal.

Number line (5)

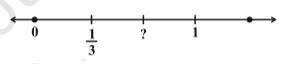
Figure shows a number line that extends on both sides of 0. Portion of the line between Numbers 0 & 1 marked on this line is divided into 3 equal parts by 2 marks. 1st of these marks is mentioned as 1/3, & a question is marked on the 2nd. By Dr TKBansal.

The point on the number line (4) which is half way between 0 and 1 has been labeled 1/2. Also, the first of the equaly spaced points that divides the distance between 0 and 1 into three equal parts can be labeled 1/3, as on number line (5). How would you label the second of these division points on number line (5)?

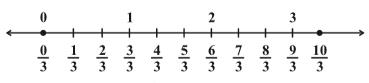
The point to be labelled is twice as far from and to the right of 0 as the point labeled 1/3. So it is two times 1/3, i.e., 2/3. You can continue to label equally-spaced points on the number line in the same way. In this continuation, the next marking is 1. You can see that 1 is the same as 3/3.

Then comes 4/3. 5/3, 6/3 (or 2), 7/3 and so on as shown on the number line (6)

Number line (6)

Figure shows a numberline that extends on both sides. Between the numbers 0 & 3 are marked numbers, 1/3, 2/3, 1, 4/3, 5/3, 2, 7/3, & 8/3, and so on. By Dr TKBansal.

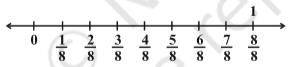
Similarly, to represent 1/8, the number line may be divided into eight equal parts as shown:

Figure shows a numberline. The portion of the line between 0 & 1 is divided in to 8 equal parts using 7 marks. Clearly the 1st mark corresponds to 1/8, 2nd to 2/8, and so on. By Dr TKBansal..

We use the number 1/8 to name the first point of this division. The second point of division will be labelled 2/8; the third point 3/8, and so on as shown on number line Figure (7)

Number line (7)
shows that the 7 marks of the previous line are marked as, 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, & 7/8. By Dr TKBansal

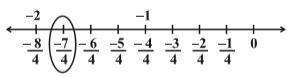
Any rational number can be represented on the number line in this way. In a rational number, the numeral below the bar, i.e., the denominator, tells the number of equal parts into which the first unit has been divided. The numeral above the bar i.e., the numerator, tells ‘how many’ of these parts are considered. So, a rational number such as 4/9 means four of nine equal parts on the right of 0 (number line 8) and for −7/4, we make 7 markings of distance 1/4 each on the left of zero and starting from 0. The seventh marking is −7/4 [number line Figure (9)].

Number line (8) 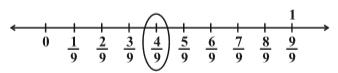Figure shows that the portion of the number line between 0 & 1 is divided into 9 equal parts and marked as 1/9, 2/9, 3/9, 4/9, .. .. 8/9. Number 4/9 is highlighted. By Dr TKBansal.

Number line (9)

Figure shows that the portion between -2 & 0 is divided into 8 equal parts & marked as, -7/8, -6/8, .. ..--1/8. the number -7/8 on the numberline is highlighted. By Dr tKBansal.

TRY THESE

Write the rational number for each point labelled with a letter.
(1)
shows a numberline with equispaced marks.They are marked as 0/5, A, 2/5, 3/5, B, C, 6/5, 7/5, D, E, 10/5, & 11/5. By Dr TKBansal.

(2)
shows a numberline with equispaced marks. they are marked as, -12/6, J, -10/6, -9/6, I, H, -6/6, G, -4/6, -3/6, F, -1/6, & 0/6. By Dr TKBansal.