NCERT Class 9 Mathematics Textbook for Blind Students made Screen Readable by Professor T K Bansal.

We have learnt in earlier classes, that rational numbers satisfy the commutative, associative and distributive laws for addition and multiplication. Moreover, if we add, subtract, multiply or divide (except by zero) two rational numbers, we still get a rational number (that is, rational numbers are ‘closed’ with respect to addition, subtraction, multiplication and division). It turns out that irrational numbers also satisfy the commutative, associative and distributive laws for addition and multiplication.

However, the sum, difference, quotients and products of irrational numbers are not always irrational. For example,

(√6) + ( − √6) , (√2) − (√2), √3 × √3 and √17÷√17 are rational numbers.

Let us look at what happens when we add and multiply a rational number with an irrational number. For example, √3 is irrational. What about 2 + √3 and 2 √3 ? Since √3 has a non-terminating non-recurring decimal expansion, the same is true for 2 + √3 and 2 √3 . Therefore, both 2 + √3 and 2 √3 are also irrational numbers.

Example 12

Check whether
7 √5 ,
7÷√5,
√2 + 21,
π −2,
are irrational numbers or not.

Solution :

√5 = 2.236... ,
√2 = 1.4142...,
π = 3.1415...

Then 7 √5 = 15.652...,
7÷√5 = (7 × √5 ÷5 = 3.1304...
√2 + 21 = 22.4142...,
Π − 2 = 1.1415...

All these are non-terminating non-recurring decimals. So, all these numbers are irrational numbers.

Now, let us see what generally happens if we add, subtract, multiply, divide, take square roots and even nth roots of these irrational numbers, where n is any natural number.

Let us look at some examples.

Example 13

Add 2 √2 + 5 √3 and √2 − 3 √3 .

Solution :

(2√2 + 5√3) + ( √2 − 3 √3)
= (2 √2 + √2 ) + (5 √3 − 3 √3)
= (2 + 1) √2 + (5 −3) √3 = 3 √2 + 2 √3

Note (by Dr T K Bansal)

that the terms with identical irrational numbers can be added like normal algebra. For instance 2 √3 + 3 √3 = 5 √3.

Example 14

Multiply 6 √5 by 2 √5 .

Solution :

6√5 × 2√5 = 6 × 2 × √5 × √5
= 12 × 5 = 60

Example 15

Divide 8 √15 by 2 √3 .

Solution :

8 √15 ÷ (2 √3)
= (8 √3 × √5)÷(2 √3)
= 4 √5

These examples may lead us to expect the following facts, which are true:
(i) The sum or difference of a rational number and an irrational number is irrational.
(ii) The product or quotient of a non-zero rational number with an irrational number is irrational.
(iii) If we add, subtract, multiply or divide two irrationals, the result may be rational or irrational.

We now turn our attention to the operation of taking √ of real numbers.

Recall that, if a is a natural number, then √a = b means b^2 = a and b > 0. The same definition can be extended for positive real numbers.

Let a > 0 be a real number, then √a = b means b^2 = a and b > 0.

In Section 1.2, we saw how to represent √n for any positive integer n on the number line. We shall now show how to find √x for any given positive real number x, geometrically.

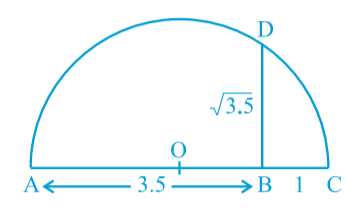
For example, let us find it for x = 3.5, i.e., we find √3.5 geometrically.

Mark the distance 3.5 units from a fixed point A on a given line to obtain a point B such that AB = 3.5 units (see Fig. 1.15). From B, mark a distance of 1 unit and mark the new point as C. Find the mid-point of AC and mark that point as O. Draw a semicircle with centre O and radius OC. Draw a line perpendicular to AC passing through B and intersecting the semicircle at D. Then, BD = square root of 3.5.

Fig. 1.15

More generally, to find √ x , for any positive real number x, we mark B so that AB = x units, and, as in Fig. 1.16, mark C so that BC = 1 unit. Then, as we have done for the case x = 3.5, we find BD = root x (see Fig. 1.16). We can prove this result using the Pythagoras Theorem.

Fig. 1.16

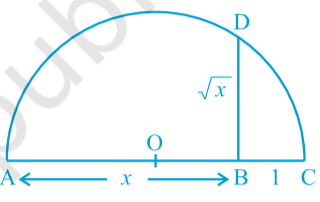
We notice that in Fig. 1.16, triangle OBD is a right-angled triangle. Also, the radius of the circle is (x+1)÷2 units. Therefore, O C = O D = OA = (x+1)÷2 units.
Now, OB = x − (x+1)÷2 = (x −1)÷2
So, by the Pythagoras Theorem, we have
BD^2 = OD^2 − OB^2 = [(x+1)÷2]^2 − [(x −1)÷2]^2 = 4x÷4 = x
This shows that BD = √x .

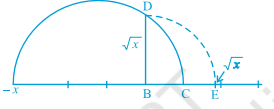
This construction gives us a visual, and symmetrical way of showing that √ x exists for all real numbers x > 0. If we want to know the position of √x on the number line, then let us treat the line BC as the number line, with B as zero, C as 1, and so on. Draw an arc with centre B and radius BD, which intersects the number line at E (see Fig. 1.17). Then, E represents √x.

Fig 1.17

We would like to now extend the idea of square roots to cube roots, fourth roots, and in general nth roots, where n is a positive integer. Recall your understanding of square roots and cube roots from earlier classes.

What is third root 8? Well, we know it has to be some positive number whose cube is 8, and you must have guessed third root 8 = 2. Let us try fifth root 243. Do you know some number b such that b^5 = 243? The answer is 3. Therefore, fifth root 243 = 3.

From these examples, can we define nth root a for a real number a > 0 and a positive integer n?

Let a > 0 be a real number and n be a positive integer. Then nth root a = b, if b^n = a and b > 0. Note that the symbol ‘ root’ used in √2, third root 8, nth root a , etc. is called the radical sign.

We now list some identities relating to square roots, which are useful in various ways. You are already familiar with some of these from your earlier classes. The remaining ones follow from the distributive law of multiplication over addition of real numbers, and from the identity (x + y) × (x − y) = x^2 − y^2, for any real numbers x and y.

Let a and b be positive real numbers. Then
(i) √(a × b) = √a × √b
ii) √(a ÷ b) = √a ÷ √b (iii) (√a + √b) × (√a − √b) = a −b
(iv) (a+ √b) × (a − √ b) = a^2 − b
(v) ( √a + √b) × ( √c+ √d) = √ac + √ad + √bc + √bd
(vi) ( √a + √b)^2 = a + B + 2√ab

Let us look at some particular cases of these identities.

Example 16

Simplify the following expressions:
(i) (5 + √7) × (2+√5)
ii) (5 + √5) × (5 − √5)
(iii) (√3 + √7)^2
(iv) (√11 − √7) × (√11 + √7)

Solution :

(i) (5 + √7) × (2 + √5) = 10 + 5√5 + 2√7 + √35
(ii) (5 + √5) × (5 − √5) = 25 − 5 =20

(iii) (√3 + √7)^2 = 3 + 2 × √21 + 7 = 10 + 2 × √21

(iv) (√11 − √7) × (√11 + √7) = (√11)^2 − (√7)^2 = 11 − 7 = 4

Remark : Note that ‘simplify’ in the example above has been used to mean that the expression should be written as the sum of a rational and an irrational number.

We end this section by considering the following problem.

Look at 1÷√2 Can you tell where it shows up on the number line?

You know that it is irrational. May be it is easier to handle if the denominator is a rational number. Let us see, if we can ‘rationalise’ the denominator, that is, to make the denominator into a rational number. To do so, we need the identities involving square roots. Let us see how.

Example 17

Rationalise the denominator of 1÷ √2.

Solution :

We want to write 1÷√2 as an equivalent expression in which the denominator is a rational number. We know that √2 × √2 is rational.

We also know that multiplying 1÷√2 by √2 ÷ √2 will give us an equivalent expression, since √2 ÷ √2 = 1. So, we put these two facts together to get

1÷√2 = 1÷√2 × √2÷√2 = √2 ÷ 2

In this form, it is easier to locate 1÷√2 on the number line. It is half way between 0 and √ 2 !

Example 18

Rationalise the denominator of 1 ÷(2+ √3)

Solution :

We use the Identity (iv) given earlier.

Multiply and divide 1 / (2 + √3) by (2 − √3) to get

1 ÷ (2 + √3) = 1 ÷ (2 + √3) × [(2 − √3) ÷ (2 − √3)] = (2 − √ 3)÷(4-3) = (2 − √ 3)

Example 19

Rationalise the denominator of 5 ÷ (√3 − √5)

Solution :

Here we use the Identity (iii) given earlier.

So, 5 ÷(√3 − √5) = 5 ÷(√3 − √5) × (√3 + √5)÷(√3 + √5) = 5 ((√3 + √5) ÷ ( 3 − 5) = ( −5÷2) ((√3 + √5)

Example 20

Rationalise the denominator of 1÷(7 + 3√2)

Solution :

1÷ (7 + 3√2) = 1÷(7 + 3√2) × (7 − 3√2)÷(7 − 3√2)
= (7 − 3√2) ÷ ( 49 -18) = (7 - 3 √ 2) ÷ 31

So, when the denominator of an expression contains a term with a √ (or a number square a radical sign), the process of converting it to an equivalent expression whose denominator is rational number is called rationalising the denominator.

EXERCISE 1.5

Q1. Classify the following numbers as rational or irrational:
(i) 2 − √5
(ii) (3 + √23) − √ 23
(iii) 2 √7÷ 7 √7
(iv) 1 ÷ √2
(v) 2 π

A1.
(i) Irrational
(ii) Rational
(iii) Rational
(iv) Irrational
(v) Irrational

Q2. Simplify each of the following expressions:
(i) (3 + √3) × (2 + √2)
(ii) (3 + √3) × (3 − √3)
(iii) (√5 + √2)^2
(iv) (√5 − √2) × (√5 + √2)

A2.
(i) 6 + 3 √2 + 2√3 + √6
(ii) 6
(iii) 7 + 2 √10
(iv) 3

Q3. Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π = c÷d. This seems to contradict the fact that π is irrational. How will you resolve this contradiction?

A3. There is no contradiction. Remember that when we measure a length with a scale or any other device, we get an approximate rational value only. So, we may not realise that either c or d is irrational.

Q4. Represent √9.3 on the number line.

A4. Refer Fig. 1.17.

Q5. Rationalise the denominators of the following:
(i) 1÷ √7
(ii) 1÷(√7 − √6)
(iii) 1÷(√5 + √2)
(iv) 1÷(√7 − 2)

A5.
(i) √7 ÷ 7
(ii) √7 + √6
(iii) (√5 − √2) ÷ 3
(iv) (√7 + 2) ÷ 3