NCERT Class 9 Mathematics Textbook for Blind Students made Screen Readable by Professor T K Bansal.

We saw, in the previous section, that there may be numbers on the number line that are not rational numbers. In this section, we are going to investigate these numbers.

So far, all the numbers WE have came across, were of the form p ÷ q , where p and q are integers and q ≠ 0. So, we may ask: are there numbers which are not of this form? There are indeed such numbers.

Start of yellow box:

<p><img alt="Figure 1.3 " src="https://blind2visionary.org/sites/all/images/ncert/class09/math/chap01/f..." style="border:5px groove gold" /></p>

Pythagoras (569 BC - 479 BC)

The Pythagoreans in Greece, followers of the famous mathematician and philosopher Pythagoras, were the first to discover the numbers which were not rational numbers, around 400 BC. These numbers are called irrational numbers (irrationals), because they cannot be written in the form of a ratio of integers. There are many myths surrounding the discovery of irrational numbers by the Pythagorean, Hippacus of Croton. In all the myths, Hippacus has an unfortunate end, either for discovering that √2 is irrational or for disclosing the secret about √2 to people outside the secret Pythagorean sect!]

End of yellow box.

Let us formally define these numbers.

A number ‘s’ is called irrational, if it cannot be written in the form p ÷ q, where p and q are integers and q ≠ 0.

We already know that there are infinitely many rational numbers. It turns out that there are infinitely many irrational numbers too. Some examples are:
√2, √3, √15, π, 0.10110111011110...

Remark : Recall that when we use the symbol √, we assume that it is the positive square root of the number. So √4 = 2, though both 2 and −2 are square roots of 4.

We are familier with some of the irrational numbers listed above are. For example, we have already come across many of the square roots listed above and the number π.

Start of yellow box:

The Pythagoreans proved that √2 is irrational. Later in approximately 425 BC, Theodorus of Cyrene showed that √3, √5, √6, √7, √10, √11, √12, √13, √14, √15 and √17 are also irrationals.

Proofs of irrationality of √2 , √3 , √5 , etc., shall be discussed in Class 10.

As to π, it was known to various cultures for thousands of years, it was proved to be irrational by Lambert and Legendre only in the late 1700s.]

End of yellow box.

In the next section, we will discuss why 0.10110111011110... and π are irrational.

Let us return to the questions raised at the end of the previous section. Remember the bag of rational numbers. If we now put all irrational numbers into the bag, will there be any number left on the number line? The answer is no! It turns out that the collection of all the rational numbers and that of irrational numbers together make up what we call the collection of real numbers, which is denoted by symbol capital R. Therefore, a real number is either rational or irrational. So, we can say that every real number is represented by a unique point on the number line. Also, every point on the number line represents a unique real number.

This is why we call the number line, the real number line.

Start of yellow box:

In the 1870’s two German mathematicians, Cantor and Dedekind, showed that :

Corresponding to every real number, there is a unique point on the real number line, and corresponding to every point on the number line, there exists a unique real number.

R. Dedekind (1831-1916)

G. Cantor (1845-1918)]

End of yellow box.

Let us see how we can locate some of the irrational numbers on the number line.

Example 3

Locate √2 on the number line.

Solution:

It is easy to see how the Greeks might have discovered √ 2. Consider a unit square OABC, with each side equals 1 unit in length (see Fig. 1.6).

Fig. 1.6

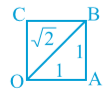
Then you can see by the Pythagoras theorem that πOB = √(1^2 + 1^2) = √2.

How do we represent √2 on the number line?

This is easy. Transfer Fig. 1.6 onto the number line making sure that the vertex O coincides with zero (see Fig. 1.7).

Fig. 1.7

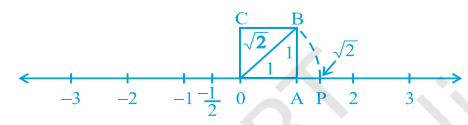
We have just seen that OB = √2. Using a compass with centre O and radius OB, draw an arc intersecting the number line at the point P. Then P corresponds to √2 on the number line.

Example 4

Locate √3 on the number line.

Solution :

Let us return to Fig. 1.7.

Fig. 1.8

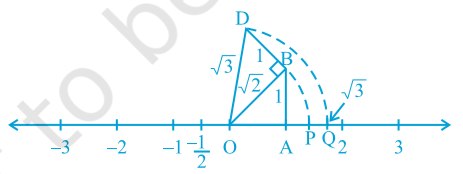
Construct BD of unit length perpendicular to OB (its diagonal of Last Square of sides having unit length). Then using the Pythagoras theorem, we see that O D = √[(√2) ^2+1^2] = √3 .

Using a compass, with centre at Point O and radius O D, draw an arc which intersects the number line at the point Q.
Then Q corresponds to √3.

In the same way, we can locate √n for any positive integer n, after √ (n − 1) has been located.

EXERCISE 1.2

Q1. State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form √m , where m is a natural number.
(iii) Every real number is an irrational number.

A1.
(i) True, since collection of real numbers is made up of rational and irrational numbers.
(ii) False, no negative number can be the √ of any natural number.
(iii) False, for example 2 is real but not irrational.

Q2. Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.

A2. No. For example, √4 = 2 is a rational number.

Q3. Show how √5 can be represented on the number line.

A3. Repeat the procedure as in Fig. 1.8 several times. First, obtain √ 4 and then √ 5.

q4. Classroom activity (Constructing the ‘ Square root spiral ’) :

Take a large sheet of paper and construct the ‘ Square root spiral ’ in the following fashion. Start with a point O and draw a line segment OP1 of unit length. Draw a line segment P1P2 perpendicular to OP1 of unit length (see Fig. 1.9).

Fig. 1.9: Constructing √ spiral

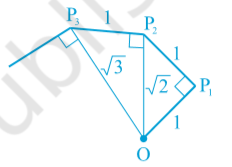
Now draw a line segment P2P3 perpendicular to OP2. Then draw a line segment P3P4 perpendicular to OP3. Continuing in this manner, you can get the line segment Pn-1Pn by drawing a line segment of unit length perpendicular to OPn−1. In this manner, you will have created the points P2, P3,...., P_n,... ., and joined them to create a beautiful spiral depicting √ 2, √ 3, √ 4, ...