NCERT Class 6 Mathematics Textbook for blind and low vision students made Screen Readable by Professor T K Bansal.

In earlier classes, we have learnt that we use centimetre (cm) as a unit of length.

For measuring the length of a pencil, the width of a book or notebooks etc., we use centimetres. Our ruler has marks on each centimetre.

For measuring the thickness of a pencil, however, we find centimetre too big.
We use millimetre (mm) to show the thickness of a pencil.
(a) 10 millimetres = 1 centimetre

To measure the length of the classroom or the school building, we shall find centimetre too small. We use metre for the purpose.
(b) 1 metre = 100 centimetres
= 1000 millimetres
Even metre is too small, when we have to state distances between cities, say, Delhi and Mumbai, or Chennai and Kolkata. For this we need kilometres (km).

Try These 1.12

Q1. How many centimetres make a kilometre?

Q2. Name five large cities in India. Find their population. Also, find the distance in kilometres between each pair of these cities

(c) 1 kilometre = 1000 metres
How many millimetres make 1 kilometre?
Since 1 m = 1000 mm
1 km = 1000 m = 1000 × 1000 mm = 10,00,000 mm

We go to the market to buy rice or wheat; we buy it in kilograms (kg). But items like ginger or chillies which we do not need in large quantities, we buy in grams (g).

We know 1 kilogram = 1000 grams.
Have you noticed the weight of the medicine tablets given to the sick? It is very small. It is in milligrams (mg).

1 gram = 1000 milligrams.

What is the capacity of a bucket for holding water? It is usually 20 litres (l). Capacity is given in litres. But sometimes we need a smaller unit, the millilitres. A bottle of hair oil, a cleaning liquid or a soft drink have labels which give the quantity of liquid inside in millilitres (ml).

1 litre = 1000 millilitres.

Note that in all these units we have some words common like kilo, milli and centi. You should remember that among these kilo is the greatest and milli is the smallest; kilo shows 1000 times greater, milli shows 1000 times smaller,

i.e. 1 kilogram = 1000 grams, 1 gram = 1000 milligrams.

Similarly, centi shows 100 times smaller, i.e. 1 metre = 100 centimetres.

Try These 1.13

Q1. How many milligrams make one kilogram?

Q2. A box contains 2,00,000 medicine tablets each weighing 20 mg. What is the total weight of all the tablets in the box in grams and in kilograms?

Try These 1.14

Q1. A bus started its journey and reached different places with a speed of 60 km/hour. The journey is shown in the figure.

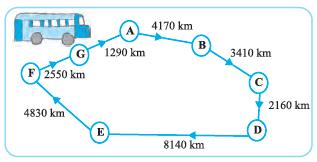
(i) Find the total distance covered by the bus from A to D.
(ii) Find the total distance covered by the bus from D to G.
(iii) Find the total distance covered by the bus, if it starts from A and returns back to A.
(iv) Can you find the difference of distances from C to D and D to E?
(v) Find out the time taken by the bus to reach
(a) A to B
(b) C to D
(c) E to G
(d) Total journey

Q2. Raman’s shop

Things	Price
Apples	Rs. 40 per kg
Oranges	Rs. 30 per kg
Combs	Rs. 3 for one
Tooth brushes	Rs. 10 for one
Pencils	Rs. 1 for one
Note books	Rs. 6 for one
Soap cakes	Rs. 8 for one

The sales during the last year

Apples	2457 kg
Oranges	3004 kg
Combs	22760
Tooth brushes	25367
Pencils	38530
Note books	40002
Soap cakes	20005

(a) Can you find the total weight of apples and oranges Raman sold last year?
Weight of apples = __________ kg
Weight of oranges = _________ kg
Therefore, total weight = _____ kg + _____ kg = _____ kg

Answer - The total weight of oranges and apples = _________ kg.

(b) Can you find the total money Raman got by selling apples?

(c) Can you find the total money Raman got by selling apples and oranges together?

(d) Make a table showing how much money Raman received from selling each item. Arrange the entries of amount of money received in descending order. Find the item which brought him the highest amount.

How much is this amount?

We have done a lot of problems that have addition, subtraction, multiplication and division. We will try solving some more here. Before starting, look at these examples and follow the methods used.

Example 1

Population of Sundarnagar was 2,35,471 in the year 1991. In the year 2001 it was found to be increased by 72,958. What was the population of the city in 2001?

Solution :

Population of the city in 2001
= Population of the city in 1991 + Increase in population
= 2,35,471 + 72,958

Now, 235471 + 72958 = 308429

Salma added them by writing 235471 as 200000 + 35000 + 471 and 72958 as 72000 + 958. She got the addition as 200000 + 107000 + 1429 = 308429.

Mary added it as 200000 + 35000 + 400 + 71 + 72000 + 900 + 58 = 308429

Answer : Population of the city in 2001 was 3,08,429.

All three methods are correct.

Example 2

In one state, the number of bicycles sold in the year 2002-2003 was 7,43,000. In the year 2003-2004, the number of bicycles sold was 8,00,100. In which year were more bicycles sold? and how many more?

Solution :

Clearly, 8,00,100 is more than 7,43,000. So, in that state, more bicycles were sold in the year 2003-2004 than in 2002-2003. 
Now, 800100 − 743000 = 057100

Check the answer by adding 743000 + 57100 800100 (the answer is right)

Can you think of alternative ways of solving this problem?
Answer : 57,100 more bicycles were sold in the year 2003-2004.

Example 3

The town newspaper is published every day. One copy has 12 pages. Everyday 11,980 copies are printed. How many total pages are printed everyday?

Solution:

Each copy has 12 pages. Hence, 11,980 copies will have 12 × 11,980 pages. What would this number be? More than 1,00,000 or lesser.

Try to estimate.

Now, 11980 × 12 = 23960 + 119800 = 143760

Answer: Everyday 1,43,760 pages are printed.

Example 4

The number of sheets of paper available for making notebooks is 75,000. Each sheet makes 8 pages of a notebook. Each notebook contains 200 pages. How many notebooks can be made from the paper available?

Solution:

Each sheet makes 8 pages.
Hence, 75,000 sheets make 8 × 75,000 pages,

Now, 75000 × 8 = 600000

Thus, 6,00,000 pages are available for making notebooks.
Now, 200 pages make 1 notebook.
Hence, 6,00,000 pages make 6,00,000 ÷ 200 notebooks.
The answer is 3,000 notebooks.

EXERCISE 1.2

Q1. A book exhibition was held for four days in a school. The number of tickets sold at the counter on the first, second, third and final day was respectively 1094, 1812, 2050 and 2751. Find the total number of tickets sold on all the four days.

A1. 7,707 tickets

Q2. Shekhar is a famous cricket player. He has so far scored 6980 runs in test matches. He wishes to complete 10,000 runs. How many more runs does he need?

A2. 3,020 runs

Q3. In an election, the successful candidate registered 5,77,500 votes and his nearest rival secured 3,48,700 votes. By what margin did the successful candidate win the election?

A3. 2,28,800 votes

Q4. Kirti bookstore sold books worth Rs. 2,85,891 in the first week of June and books worth Rs. 4,00,768 in the second week of the month. How much was the sale for the two weeks together? In which week was the sale greater and by how much?

A4. Rs. 6,86,659; second week, Rs. 1,14,877

Q5. Find the difference between the greatest and the least 5-digit number that can be written using the digits 6, 2, 7, 4, 3 each only once.

A5. 52,965

Q6. A machine, on an average, manufactures 2,825 screws a day. How many screws did it produce in the month of January 2006?

A6.7,575 screws

Q7. A merchant had Rs.78,592 with her. She placed an order for purchasing 40 radio sets at Rs.1200 each. How much money will remain with her after the purchase?

A7. Rs. 30,592

Q8. A student multiplied 7236 by 65 instead of multiplying by 56. By how much was his answer greater than the correct answer?
(Hint: Do you need to do both the multiplications?)

A8. 65,124

Q9. To stitch a shirt, 2 m 15 cm cloth is needed. Out of 40 m cloth, how many shirts can be stitched and how much cloth will remain?
(Hint: convert data in cm.)

A9. 18 shirts, 1 m 30 cm

Q10. Medicine is packed in boxes, each weighing 4 kg 500g. How many such boxes can be loaded in a van which cannot carry beyond 800 kg?

A10. 177 boxes

Q11. The distance between the school and a student’s house is 1 km 875 m. Everyday she walks both ways. Find the total distance covered by her in six days.

A11. 22 km 500 m

Q12. A vessel has 4 litres and 500 ml of curd. In how many glasses, each of 25 ml capacity, can it be filled?

A12. 180 glasses

1.3.1 Estimation

News Items

1. India drew with Pakistan in a hockey match watched by approximately 51,000 spectators in the stadium and 40 million television viewers worldwide.

2. Approximately, 2000 people were killed and more than 50000 injured in a cyclonic storm in coastal areas of India and Bangladesh.

3. Over 13 million passengers are carried over 63,000 kilometre route of railway track every day.

Can we say that there were exactly as many people as the numbers quoted in these news items?

For example,
In (1), were there exactly 51,000 spectators in the stadium? or did exactly 40 million viewers watched the match on television?
Obviously, not. The word approximately itself shows that the number of people were near about these numbers. Clearly, 51,000 could be 50,800 or 51,300 but not 70,000. Similarly, 40 million implies much more than 39 million but quite less than 41 million but certainly not 50 million.

The quantities given in the examples above are not exact counts, but are estimates to give an idea of the quantity.

Discuss what each of these can suggest.

Where do we approximate? Imagine a big celebration at your home. The first thing you do is to find out roughly how many guests may visit you. Can you get an idea of the exact number of visitors? It is practically impossible.

The finance minister of the country presents a budget annually. The minister provides for certain amount under the head ‘Education’. Can the amount be absolutely accurate?

It can only be a reasonably good estimate of the expenditure the country needs for education during the year.

Think about the situations where we need to have the exact numbers and compare them with situations where you can do with only an approximately estimated number.

Give three examples of each of such situations.

1.3.2 Estimating to the nearest tens by rounding off

Look at the following :
(a) Find which flags are closer to 260.
(b) Find the flags which are closer to 270.

Locate the numbers 10,17 and 20 on your ruler. Is 17 nearer to 10 or 20? The gap between 17 and 20 is smaller when compared to the gap between 17 and 10.

So, we round off 17 as 20, correct to the nearest tens.
Now consider 12, which also lies between 10 and 20. However, 12 is closer to 10 than to 20. So, we round off 12 to 10, correct to the nearest tens.
How would you

Try these 1.15

Round these numbers to the nearest tens.
28, 32, 52, 41, 39, 48, 64, 59, 99, 215, 1453, 2936.

1.3.3 Estimating to the nearest hundreds by rounding off

Is 410 nearer to 400 or to 500?

410 is closer to 400, so it is rounded off to 400, correct to the nearest hundred.

889 lies between 800 and 900.

It is nearer to 900, so it is rounded off as 900 correct to nearest hundred.

Numbers 1 to 49 are closer to 0 than to 100, and so are rounded off to 0.
Numbers 51 to 99 are closer to 100 than to 0, and so are rounded off to 100.
Number 50 is equidistant both from 0 and 100. It is a common practice to round it off as 100.

Check if the following rounding off is correct or not :
841 → 800;
9537 → 9500;
49730 → 49700;
2546 → 2500;
286 → 200;
5750 → 5800;
168 → 200;
149 → 100;
9870 → 9800.

Correct those which are wrong.

1.3.4 Estimating to the nearest thousands by rounding off

We know that numbers 1 to 499 are nearer to 0 than to 1000, so these numbers are rounded off as 0.

The numbers 501 to 999 are nearer to 1000 than 0 so they are rounded off as 1000.

Number 500 is also rounded off as 1000.

Check if the following rounding off is correct or not :
2573 → 3000;
53552 → 53000;
6404 →6000;
65437 →65000;
7805 → 7000;
3499 → 4000.
Correct those which are wrong.

Try These 1.16

Round off the given numbers to the nearest tens, hundreds and thousands.

Given Number	Approximate to Nearest	Rounded Form
75847	Tens	________________
75847	Hundreds	________________
75847	Thousands	________________
75847	Ten thousands	________________

1.3.5 Estimating outcomes of number situations

How do we add numbers? We add numbers by following the algorithm (i.e. the given method) systematically. We write the numbers taking care that the digits in the same place (ones, tens, hundreds etc.) are in the same column.

For example,
3946 + 6579 + 2050 is written as -

 

Th	H	T	O
3	9	4	6
6	5	7	9
+
2	0	5	0

We add the column of ones and if necessary carry forward the appropriate number to the tens place as would be in this case. We then add the tens column and this goes on. Complete the rest of the sum yourself. This procedure takes time.

There are many situations where we need to find answers more quickly.

For example, when you go to a fair or the market, you find a variety of attractive things which you want to buy. You need to quickly decide what you can buy. So, you need to estimate the amount you need. It is the sum of the prices of things you want to buy.A trader is to receive money from two sources. The money he is to receive is Rs. 13,569 from one source and Rs. 26,785 from another. He has to pay Rs. 37,000 to someone else by the evening. He rounds off the numbers to their nearest thousands and quickly works out the rough answer. He is happy that he has enough money.

Do you think he would have enough money? Can you tell without doing the exact addition/subtraction?

Sheila and Mohan have to plan their monthly expenditure. They know their monthly expenses on transport, on school requirements, on groceries, on milk, and on clothes and also on other regular expenses. This month they have to go for visiting and buying gifts. They estimate the amount they would spend on all this and then add to see, if what they have, would be enough.

Would they round off to thousands as the trader did?
Think and discuss five more situations where we have to estimate sums or remainders.

Did we use rounding off to the same place in all these?
There are no rigid rules when you want to estimate the outcomes of numbers. The procedure depends on the degree of accuracy required and how quickly the estimate is needed. The most important thing is, how sensible the guessed answer would be.

1.3.6 To estimate sum or difference

As we have seen above we can round off a number to any place. The trader rounded off the amounts to the nearest thousands and was satisfied that he had enough. So, when you estimate any sum or difference, you should have an idea of why you need to round off and therefore the place to which you would round off. Look at the following examples.

Example 5

Estimate: 5,290 + 17,986.

Solution:

You find 17,986 > 5,290.
Round off to thousands.
17,986 rounds off to 18,000
+5,290 rounds off to + 5,000
Estimated sum = 23,000

Does the method work? You may attempt to find the actual answer and verify if the estimate is reasonable.

Example 6

Estimate: 5,673 − 436.

Solution:
To begin with we round off to thousands. (Why?)
5,673 rounds off to 6,000
− 436 rounds off to − 0
Estimated difference = 6,000
This is not a reasonable estimate. Why is this not reasonable?

To get a closer estimate, let us try rounding each number to hundreds.
5,673 rounds off to 5,700
− 436 rounds off to − 400
Estimated difference = 5,300
This is a better and more meaningful estimate.

1.3.7 To estimate products

How do we estimate a product?
What is the estimate for 19 × 78?
It is obvious that the product is less than 2000. Why?

If we approximate 19 to the nearest tens, we get 20 and then approximate 78 to nearest tens, we get 80 and 20 × 80 = 1600

Look at 63 × 182
If we approximate both to the nearest hundreds we get 100 × 200 = 20,000. This is much larger than the actual product. So, what do we do? To get a more reasonable estimate, we try rounding off 63 to the nearest 10,

i.e. 60, and also 182 to the nearest ten,
i.e. 180. We get 60 × 180 or 10,800.

Try These 1.17

Estimate the
following products :
(a) 87 × 313
(b) 9 × 795
(c) 898 × 785
(d) 958 × 387

Make five more such problems and solve them.

This is a good estimate, but is not quick enough. If we now try approximating 63 to 60 and 182 to the nearest hundred, i.e. 200, we get 60 × 200, and this number 12,000 is a quick as well as good estimate of the product.

The general rule that we can make is, therefore, Round off each factor to its greatest place, then multiply the rounded off factors. Thus, in the above example, we rounded off 63 to tens and 182 to hundreds.

Now, estimate 81 × 479 using this rule : 479 is rounded off to 500 (rounding off to hundreds), and 81 is rounded off to 80 (rounding off to tens).

The estimated product = 500 × 80 = 40,000
An important use of estimates for you will be to check your answers.
Suppose, you have done the multiplication 37 × 1889, but are not sure about your answer. A quick and reasonable estimate of the product will be 40 × 2000 i.e. 80,000. If your answer is close to 80,000, it is probably right. On the other hand, if it is close to 8000 or 8,00,000, something is surely wrong in your multiplication.

Same general rule may be followed by addition and subtraction of two or more numbers.

EXERCISE 1.3

Q1. Estimate each of the following using general rule:
(a) 730 + 998
(b) 796 − 314
(c) 12,904 +2,888
(d) 28,292 − 21,496

Make ten more such examples of addition, subtraction and estimation of their outcome.

A1. (a) 1,700
(b) 500
(c) 16,000
(d) 7,000

Q2. Give a rough estimate (by rounding off to nearest hundreds) and also a closer estimate (by rounding off to nearest tens) :
(a) 439 + 334 + 4,317
(b) 1,08,734 − 47,599
(c) 8325 − 491
(d) 4,89,348 − 48,365

Make four more such examples.

A2. (a) 5,000 ; 5,090
(b) 61,100 ; 61,130
(c) 7,800 ; 7,840
(d) 4,40,900 ; 4,40,980

Q3. Estimate the following products using general rule:
(a) 578 × 161
(b) 5281 × 3491
(c) 1291 × 592
(d) 9250 × 29

Make four more such examples.

A3. (a) 1,20,000
(b) 1,75,00,000
(c) 7,80,000
(d) 3,00,000