NCERT Class 6 Mathematics Textbook for low vision and blind students made Screen Readable by Professor T K bansal..

As we have done quite a lot of this earlier, let us see if we remember which is the greatest among these:

(i) 92, 392, 4456, 89742
(ii) 1902, 1920, 9201, 9021, 9210

So, we know the answers.

Discuss with your friends, how you find the number that is the greatest.

Try These 1.1

Can you instantly find the greatest and the smallest numbers in each of the following rows?

Q1. 382, 4972, 18, 59785, 750.
A1. 59785 is the greatest and 18 is the smallest.

Q2. 1473, 89423, 100, 5000, 310.
A2. ________________

Q3. 1834, 75284, 111, 2333, 450.
A3. ___

Q4. 2853, 7691, 9999, 12002, 124.
A4. ____

Was that easy? Why was it easy? We just looked at the number of digits and found the answer. The greatest number has the most thousands and the smallest is only in hundreds or in tens.

Make five more problems of this kind and give to your friends to solve.

Now, how do we compare 4875 and 3542?

This is also not very difficult. These two numbers have the same number of digits. They are both in thousands. But the digit at the thousands place in 4875 is greater than that in 3542. Therefore, 4875 is greater than 3542.

Next, tell which is greater, 4875 or 4542? Here too the numbers have the same number of digits. Further, the digits at the thousands place are same in both. What do we do then? We move to the next digit, that is to the digit at the hundreds place. The digit at the hundreds place is greater in 4875 than in 4542.
Therefore, 4875 is greater than 4542.

Try These 1.2

Find the greatest and the smallest numbers out of the following numbers.
(a) 4536, 4892, 4370, 4452.
(b) 15623, 15073, 15189, 15800.
(c) 25286, 25245, 25270, 25210.
(d) 6895, 23787, 24569, 24659.

If the digits at hundreds place are also same in the two numbers, then what do we do?

Compare 4875 and 4889 ; Also compare 4875 and 4879.

1.2.1 How many numbers can you make?

Suppose, we have four digits 7, 8, 3, 5. Using these digits we want to make
Different 4-digit numbers in such a way that no digit is repeated in them. Thus,
7835 is allowed, but 7735 is not. Make as many 4-digit numbers as you can.
Which is the greatest number you can get? Which is the smallest number?
The greatest number is 8753 and the smallest is 3578.
Think about the arrangement of the digits in both. Can you say how the largest number is formed? Write down your procedure.

Try These 1.3

Q1. Use the given digits without repetition and make the greatest and smallest 4-digit numbers.
(a) 2, 8, 7, 4
(b) 9, 7, 4, 1
(c) 4, 7, 5, 0
(d) 1, 7, 6, 2
(e) 5, 4, 0, 3
(Hint : 0754 is a 3-digit number.)

Q2. Now make the greatest and the smallest 4-digit numbers by using any one digit twice.
(a) 3, 8, 7
(b) 9, 0, 5
(c) 0, 4, 9
(d) 8, 5, 1.
(Hint : Think in each case which digit will you use twice.)

Q3. Make the greatest and the smallest 4-digit numbers using any four different digits with conditions as given.

(a) Digit 7 is always at ones place

Greatest: 9867

Smallest: 1027

Note, the number cannot begin with the digit 0. Why?)

(b) Digit 4 is always at tens place

Greatest: 9847

Smallest: 1042

(c) Digit 9 is always at hundreds place

Greatest: 8976.

Smallest: 1923.

(d) Digit 1 is always at thousands place

Greatest: 1987.

Smallest: 1234.

Q4. Take two digits, say 2 and 3. Make 4-digit numbers using both the digits equal number of times.
Which is the greatest number?
Which is the smallest number?
How many different numbers can you make in all?

Stand in proper order

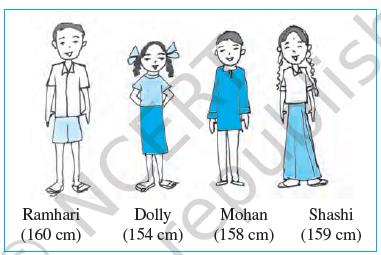
Q1. Who is the tallest?
Q2. Who is the shortest?
(a) Can you arrange them in the increasing order of their heights?
(b) Can you arrange them in the decreasing order of their heights?

Which to buy?

Sohan and Rita went to buy an almirah. There were many almirahs available with their price tags.

Image:

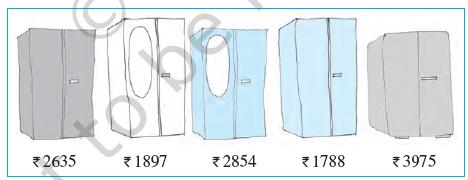
(a) Can you arrange their prices in increasing order?
(b) Can you arrange their prices in decreasing order?

Try These 1.4

Think of five more situations where you compare three or more quantities.

Ascending order

Ascending order means arrangement from the smallest to the greatest.

Descending order

Descending order means arrangement from the greatest to the smallest.

Try These 1.5

Q1. Arrange the following numbers in ascending order :
(a) 847, 9754, 8320, 571
(b) 9801, 25751, 36501, 38802

Q2. Arrange the following numbers in descending order :
(a) 5000, 7500, 85400, 7861
(b) 1971, 45321, 88715, 92547

Make ten such examples of ascending/descending order and solve them.

1.2.2 Shifting digits

Have you thought what fun it would be if the digits in a number could shift (move) from one place to the other?

Think about what would happen to 182. It could become as large as 821 and as small as 128.
Try this with 391 as well.

Now think about this.
Take any 3-digit number and exchange the digit at the hundreds place with the digit at the ones place.

(a) Is the new number greater than the former one?
(b) Is the new number smaller than the former number?
Write the numbers formed in both ascending and descending order.

Before: 795

Exchanging the 1st and the 3rd tiles.

After: 597

If you exchange the 1st and the 3rd tiles (i.e. digits), in which case does the number become greater? In which case does it become smaller?

Try this with a 4-digit number.

1.2.3 Introducing 10,000

We know that beyond 99 there is no 2-digit number. 99 is the greatest 2-digit number. Similarly, the greatest 3-digit number is 999 and the greatest 4-digit number is 9999. What shall we get if we add 1 to 9999?
Look at the pattern : 9 + 1 = 10 = 10 × 1
99 + 1 = 100 = 10 × 10
999 + 1 = 1000 = 10 × 100
We observe that
Greatest single digit number + 1 = smallest 2-digit number
Greatest 2-digit number + 1 = smallest 3-digit number
Greatest 3-digit number + 1 = smallest 4-digit number
We should then expect that on adding 1 to the greatest 4-digit number, we would get the smallest 5-digit number, that is
9999 + 1 = 10000.

The new number which comes next to 9999 is 10000. It is called ten thousand. Further,
10000 = 10 × 1000.

1.2.4 Revisiting place value

You have done this quite earlier, and you will certainly remember the expansion of a 2-digit number like 78 as
78 = 70 + 8 = 7 × 10 + 8

Similarly, you will remember the expansion of a 3-digit number like 278 as
278 = 200 + 70 + 8 = 2 × 100 + 7 × 10 + 8
We say, here, 8 is at ones place, 7 is at tens place and 2 at hundreds place.
Later on we extended this idea to 4-digit numbers.

For example, the expansion of 5278 is
5278 = 5000 + 200 + 70 + 8
= 5 × 1000 + 2 × 100 + 7 × 10 + 8
Here, 8 is at ones place, 7 is at tens place, 2 is at hundreds place and 5 is at thousands place.

With the number 10000 known to us, we may extend the idea further. We may write 5-digit numbers like

45278 = 4 × 10000 + 5 × 1000 + 2 × 100 + 7 × 10 + 8
We say that here 8 is at ones place, 7 at tens place, 2 at hundreds place, 5 at thousands place and 4 at ten thousands place.
The number is read as forty five thousand, two hundred seventy eight.
Can you now write the smallest and the greatest 5-digit numbers?

Try These 1.6

Read and expand the numbers wherever there are blanks.

Number	Number Name	Expansion
20000	twenty thousand	2 × 10000
26000	twenty six thousand	2 × 10000 + 6 × 1000
38400	thirty eight thousand four hundred	3 × 10000 + 8 × 1000 + 4 × 100
65740	sixty five thousand seven hundred forty	6 × 10000 + 5 × 1000 + 7 × 100 + 4 × 10
89324	eighty nine thousand three hundred twenty four	8 × 10000 + 9 × 1000 + 3 × 100 + 2 × 10 + 4 × 1
50000	_______________	_______________
41000	_______________	_______________
47300	_______________	_______________
57630	_______________	_______________
29485	_______________	_______________
29085	_______________	_______________
20085	_______________	_______________
20005	_______________	_______________

Write five more 5-digit numbers, read them and expand them.

1.2.5 Introducing 100,000

Which is the greatest 5-digit number?

Adding 1 to the greatest 5-digit number, should give the smallest 6-digit number :
99,999 + 1 = 100,000

This number is named one lakh. One lakh comes next to 99,999.
10 × 10,000 = 1,00,000
We may now write 6-digit numbers in the expanded form as
2,46,853 = 2 × 1,00,000 + 4 × 10,000 + 6 × 1,000 + 8 × 100 + 5 × 10 +3 × 1

This number has 3 at ones place, 5 at tens place, 8 at hundreds place, 6 at thousands place, 4 at ten thousands place and 2 at lakh place.
Its number name is two lakh forty six thousand eight hundred fifty three.

Try these 1.7

Read and expand the numbers wherever there are blanks

Number	Number Name	Expansion
3,00,000	three lakh	3 × 1,00,000
3,50,000	three lakh fifty thousand	3 × 1,00,000 + 5 × 10,000
3,53,500	three lakh fifty three thousand five hundred	3 × 1,00,000 + 5 × 10,000 + 3 × 1000 + 5 × 100
4,57,928	_______________	_______________
4,07,928	_______________	_______________
4,00,829	_______________	_______________
4,00,029	_______________	_______________

1.2.6 Larger numbers

If we add one more to the greatest 6-digit number we get the smallest 7-digit number. It is called ten lakh.

Write down the greatest 6-digit number and the smallest 7-digit number.

Write the greatest 7-digit number and the smallest 8-digit number.
The smallest 8-digit number is called one crore.

Complete the pattern :
9 + 1 = 10
99 + 1 = 100
999 + 1 = _______
9,999 + 1 = _______
99,999 + 1 = _______
9,99,999 + 1 = _______
99,99,999 + 1 = 1,00,00,000

Remember:
1 hundred = 10 tens
1 thousand = 10 hundreds
= 100 tens

1 lakh = 100 thousands
= 1000 hundreds

1 crore = 100 lakhs
= 10,000 thousands

Try These 1.8

Q1. What is 10 − 1 =?
Q2. What is 100 − 1 =?
Q3. What is 10,000 − 1 =?
Q4. What is 1,00,000 − 1 =?
Q5. What is 1,00,00,000 − 1 =?
(Hint : Use the said pattern.)

Large Numbers:

We come across large numbers in many different situations. For example, while the number of children in your class would be a 2-digit number, the number of children in your school would be a 3 or 4-digit number.

The number of people in the nearby town would be much larger.
Is it a 5 or 6 or 7-digit number?
Do you know the number of people in your state?
How many digits would that number have?
What would be the number of grains in a sack full of wheat? A 5-digit number, a 6-digit number or more?

Try These 1.9

Q1. Give five examples where the number of things counted would be more than 6-digit number.
Q2. Starting from the greatest 6-digit number, write the previous five numbers in descending order.
Q3. Starting from the smallest 8-digit number, write the next five numbers in ascending order and read them.

1.2.7 An aid in reading and writing large numbers

Try reading the following numbers :
(a) 279453
(b) 5035472
(c) 152700375
(d) 40350894

Was it difficult?
Did you find it difficult to keep track?

Sometimes it helps to use indicators to read and write large numbers.
Shagufta uses indicators which help her to read and write large numbers.
Her indicators are also useful in writing the expansion of numbers.

For example, she identifies the digits in ones place, tens place and hundreds place in 257 by writing them under the tables O, T and H as

H = 2, T = 5, O = 7

Expansion: 2 × 100 + 5 × 10 + 7 × 1

Similarly, for 2902,
Th = 2, H = 9, T = 0, O = 2
Expansion: 2 × 1000 + 9 × 100 + 0 × 10 + 2 × 1

One can extend this idea to numbers upto lakh as seen in the following table. (Let us call them placement boxes). Fill the entries in the blanks left.

Number	T Lakh	Lakh	TTh	Th	H	T	O	Number Name	Expansion
7,34,543	___	7	3	4	5	4	3	Seven lakh thirty four thousand five hundred forty three	___
32,75,829	3	2	7	5	8	2	9	___	3 × 10,00,000 + 2 × 1,00,000 + 7 × 10,000 + 5 × 1000 + 8 × 100 + 2 × 10 + 9

Similarly, we may include numbers upto crore as shown below :

Number	TCr	Cr	TLakh	Lakh	TTh	Th	H	T	O	Number Name
2,57,34,543	-	2	5	7	3	4	5	4	3	____
65,32,75,829	6	5	3	2	7	5	8	2	9	Sixty five crore thirty two lakh seventy five thousand eight hundred twenty nine

You can make other formats of tables for writing the numbers in expanded form.

Use of commas

You must have noticed that in writing large numbers in the sections above, we have often used commas. Commas help us in reading and writing large numbers. In our Indian System of Numeration we use ones, tens, hundreds, thousands and then lakhs and crores. Commas are used to mark thousands, lakhs and crores. The first comma comes after hundreds place (three digits from the right) and marks thousands. The second comma comes two digits later (five digits from the right). It comes after ten thousands place and marks lakh. The third comma comes after another two digits (seven digits from the right). It comes after ten lakh place and marks crore.

While writing number names, we do not use commas.

For example, 5, 08, 01, 592; 3, 32, 40, 781; 7, 27, 05, 062

Try reading the numbers given above. Write five more numbers in this form and read them.

International System of Numeration

In the International System of Numeration, as it is being used we have ones, tens, hundreds, thousands and then millions. One million is a thousand thousands. Commas are used to mark thousands and millions. It comes after every three digits from the right. The first comma marks thousands and the next comma marks millions.
For example, the number 50,801,592 is read
in the International System as fifty million eight hundred one thousand five hundred ninety two.
In the Indian System, it is five crore eight lakh one thousand five hundred ninety two.

How many lakhs make a million?
How many millions make a crore?
Take three large numbers. Express them in both Indian and International Numeration systems.

An Interesting fact :

To express numbers larger than a million, a billion is used in the International System of Numeration: 1 billion = 1000 million.

How much was the increase in population during 1991-2001? Try to find out.
Do you know what is India’s population today? Try to find this too.

Do you know?

India’s population increased by about
27 million during 1921-1931;
37 million during 1931-1941;
44 million during 1941-1951;
78 million during 1951-1961!

Try These 1.10

Q1. Read these numbers. Write them using placement boxes and then write their expanded forms.
(i) 475320
(ii) 9847215
(iii) 97645310
(iv) 30458094

(a) Which is the smallest number?
(b) Which is the greatest number?
(c) Arrange these numbers in ascending and descending orders.

Q2. Read these numbers.
(i) 527864
(ii) 95432
(iii) 18950049
(iv) 70002509

(a) Write these numbers using placement boxes and then using commas in Indian as well as International System of Numeration..
(b) Arrange these in ascending and descending order.

Q3. Take three more groups of large numbers and do the exercise given above.

Can you help me write the numeral?
To write the numeral for a number you can follow the boxes again.
(a) Forty two lakh seventy thousand eight.
(b) Two crore ninety lakh fifty five thousand eight hundred.
(c) Seven crore sixty thousand fifty five.

Try these 1.11

Q1. You have the following digits 4, 5, 6, 0, 7 and 8. Using them, make five numbers each with 6 digits.
(a) Put commas for easy reading.
(b) Arrange them in ascending and descending order.

Q2. Take the digits 4, 5, 6, 7, 8 and 9. Make any three numbers each with 8 digits. Put commas for easy reading.

Q3. From the digits 3, 0 and 4, make five numbers each with 6 digits. Use commas.

EXERCISE 1.1

Q1. Fill in the blanks:
(a) 1 lakh = _______ ten thousand.
(b) 1 million = _______ hundred thousand.
(c) 1 crore = _______ ten lakh.
(d) 1 crore = _______ million.
(e) 1 million = _______ lakh.

A1. (a) Ten
(b) Ten
(c) Ten
(d) Ten
(e) Ten

Q2. Place commas correctly and write the numerals:
(a) Seventy three lakh seventy five thousand three hundred seven.
(b) Nine crore five lakh forty one.
(c) Seven crore fifty two lakh twenty one thousand three hundred two.
(d) Fifty eight million four hundred twenty three thousand two hundred two.
(e) Twenty three lakh thirty thousand ten.

A2. (a) 73,75,307
(b) 9,05,00,041
(c) 7,52, 21,302
(d) 58,423,202
(e) 23,30,010

Q3. Insert commas suitably and write the names according to Indian System of Numeration :
(a) 87595762
(b) 8546283
(c) 99900046
(d) 98432701

A3.
(a) 8,75,95,762 : Eight crore seventy-five lakh ninety-five thousand seven hundred sixty two.
(b) 85,46,283 : Eighty-five lakh forty-six thousand two hundred eighty-three.
(c) 9,99,00,046: Nine crore ninety-nine lakh forty six.
(d) 9,84,32,701: Nine crore eighty-four lakh, thirty-two thousand seven hundred one.

Q4. Insert commas suitably and write the names according to International System of Numeration :
(a) 78921092
(b) 7452283
(c) 99985102
(d) 48049831

A4.
(a) 78,921,092: Seventy eight million, nine hundred twenty one thousand, ninety two.
(b) 7,452,283: Seven million four hundred fifty two thousand two hundred eighty three.
(c) 99,985,102: Ninety nine million nine hundred eighty five thousand, one hundred two.
(d) 48,049,831: Forty eight million forty nine thousand eight hundred thirty one.