NCERT Class 6 Mathematics Text book for Blind Students made Screen Readable by Professor T K Bansal.

Let us now see how certain common rules in mathematics that we have already learnt are expressed using variables.

11.6.1 Rules from geometry

We have already learnt about the perimeter of a square and of a rectangle in the chapter on Mensuration. Here, we go back to them to write them in the form of a rule.

1. Perimeter of a square

We know that perimeter of any polygon (a closed figure made up of 3 or more line segments) is the sum of the lengths of its sides.

A square has 4 sides and they are equal in length

Fig.11.8

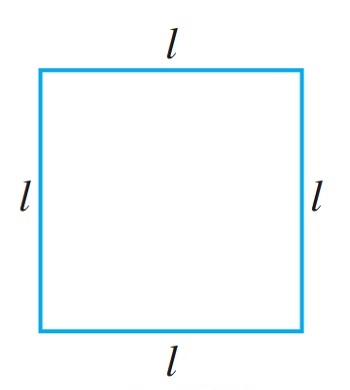
Therefore, The perimeter of a square = Sum of the lengths of the sides of the square
= 4 × the length of a side of the square
= 4 × l = 4l

Thus, we get the rule for the perimeter of a square. The use of the variable l allows us to write the general rule in a way that is concise and easy to remember.

We may take the perimeter also to be represented by a variable, say p. Then the rule for the perimeter of a square is expressed as a relation between the perimeter and the length of the square,

p = 4l

Fig. 11.9

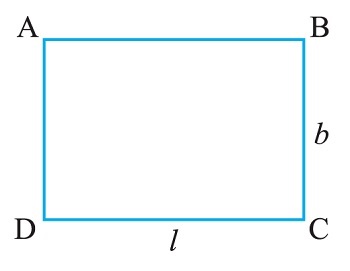
2. Perimeter of a rectangle

We know that a rectangle has four sides. For example, the rectangle ABCD has four sides AB, BC, CD and DA. The opposite sides of any rectangle are always equal in length. Thus, in the rectangle ABCD, let us denote the length by l, and, by b, the length of the sides AD or BC. Therefore,

Perimeter of a rectangle = length of AB + length of BC + length of CD + length of AD
= 2 × length of CD + 2 × length of BC = 2l + 2b

The rule, therefore, is that the perimeter of a rectangle = 2l + 2b
where, l and b are respectively the length and breadth of the rectangle.

Discuss what happens if l = b.

If we denote the perimeter of the rectangle by the variable p, the rule for perimeter of a rectangle becomes

p = 2l + 2b

Start of blue box

Note : Here, both l and b are variables. They take on values independent of each other, i.e. the value one variable takes does not depend on what value the other variable has taken.

End of blue box

In your studies of geometry you will come across several rules and formulas dealing with perimeters and areas of plane figures, and surface areas and volumes of three-dimensional figures. Also, you may obtain formulas for the sum of internal angles of a polygon, the number of diagonals of a polygon and so on. The concept of variables which you have learnt will prove very useful in writing all such general rules and formulas.

11.6.2 Rules from arithmetic

3. Commutativity of addition of two numbers

We know that

4 + 3 = 7 and 3 + 4 = 7

i.e. 4 + 3 = 3 + 4

As we have seen in the chapter on whole numbers, this is true for any two numbers. This property of numbers is known as the commutativity of addition of numbers. Commuting means interchanging. Commuting the order of numbers in addition does not change the sum. The use of variables allows us to express the generality of this property in a concise way.

Let a and b be two variables which can take any number value.

Then, a + b = b + a

Once we write the rule in this way, all special cases are included in it.
If a = 4 and b = 3, we get 4 + 3 = 3 + 4.
If a = 37 and b = 73, we get 37 + 73 = 73 + 37 and so on.

4. Commutativity of multiplication of two numbers

We have seen in the chapter on whole numbers that for multiplication of two numbers, the order of the two numbers being multiplied does not matter. 

For example, 4 × 3 = 12, and 3 × 4 = 12

Hence, 4 × 3 = 3 × 4

This property of numbers is known as commutativity of multiplication of numbers. Commuting (interchanging) the order of numbers in multiplication does not change the product. Using variables a and b as in the case of addition, we can express the commutativity of multiplication of two numbers as a × b = b × a

Note that a and b can take any number value. They are variables. All the special cases like

4 × 3 = 3 × 4 or 37 × 73 = 73 × 37 follow from the general rule.

5. Distributivity of numbers

Suppose we are asked to calculate 7 × 38. We obviously do not know the table of 38. So, we do the following:

7 × 38 = 7 × (30 + 8) = 7 × 30 + 7 × 8 = 210 + 56 = 266

This is always true for any three numbers like 7, 30 and 8. This property is known as distributivity of multiplication over addition of numbers.

By using variables, we can write this property of numbers also in a general and concise way.

Let a, b and c be three variables, each of which can take any number. Then, a × (b + c) = a × b + a × c

Properties of numbers are fascinating. You will learn many of them in your study of numbers this year and in your later study of mathematics.

Use of variables allows us to express these properties in a very general and concise way. One more property of numbers is given in question 5 of Exercise 11.2. Try to find more such properties of numbers and learn to express them using variables.

EXERCISE 11.2

Q1. The side of an equilateral triangle is shown by l. Express the perimeter of the equilateral triangle using l.

Fig.11.10

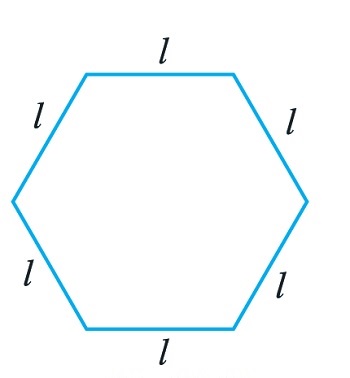
Q2. The side of a regular hexagon (Fig 11.10) is denoted by l. Express the perimeter of the hexagon using l. (Hint: A regular hexagon has all its six sides equal in length.)

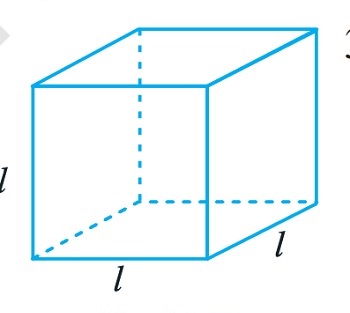
Q3. A cube is a three-dimensional figure as shown in Fig 11.11. It has six faces and all of them are identical squares. The length of an edge of the cube is given by l. Find the formula for the total length of the edges of a cube.

Fig 11.11 

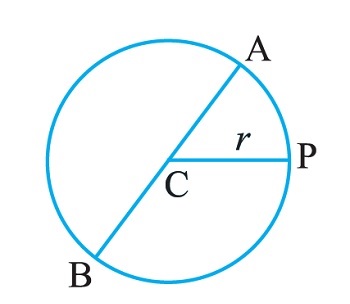
Q4. The diameter of a circle is a straight line which joins two points on the circle, and also passes through the centre of the circle. (In the adjoining figure (Fig 11.12) AB is a diameter of the circle; C is its centre.) Express the diameter of the circle (d) in terms of its radius (r).

Fig. 11.12

Q5. To find sum of three numbers 14,27 and 13, we can have two ways:
(a) We may first add 14 and 27 to get 41 and then add 13 to it to get the total sum 54 or
(b) We may add 27 and 13 to get 40 and then add 14 to get the sum 54.
Thus, (14 + 27) + 13 = 14 + (27 + 13)
This can be done for any three numbers. This property is known as the associativity of addition of numbers. Express this property which we have already studied in the chapter on Whole Numbers, in a general way, by using variables a, b and c.