NCERT Class 6 Mathematics Textbook in Hindi for Blind Students made Screen Readable by Professor T K Bansal.

चूँकि हम संख्याओं की तुलना पहले भी बहुत कर चुके हैं, आइए देखें कि क्या हमें याद है कि दी गई संख्याओं में कौन सी संख्या सबसे बड़ी है?
(i) 92, 392, 4456; मे 89742 सबसे बड़ी है.
(ii) 1902, 1920, 9201, 9021; मैं 9210 सबसे बड़ी है.

तो, हम यहाँ उत्तर जानते हैं।
अपने मित्रों में चर्चा कीजिए और पता कीजिए कि किसी संख्या समूह में वे सबसे बड़ी संख्या किस प्रकार ज्ञात करते हैं।

प्रयास कीजिए

क्या आप तुरंत ज्ञात कर सकते हैं कि प्रत्येक पंक्ति में कौन सी संख्या सबसे बड़ी है और कौन सी संख्या सबसे छोटी है?

(1) 382, 4972, 18, 59785, 750
उत्तर : 59785 सबसे बड़ी है और 18 सबसे छोटी है।

(2) 1473, 89423, 100, 5000, 310
उत्तर : (रिक्त स्थान)

(3) 1834, 75284, 111, 2333, 450
उत्तर : (रिक्त स्थान)

(4) 2853, 7691, 9999, 12002, 124
उत्तर : (रिक्त स्थान)

क्या यह सरल था? यह सरल क्यों था?

यहाँ हमने केवल अंकों की संख्या को देखकर ही उत्तर ज्ञात कर लिया। सबसे बड़ी संख्या में अधिकतम हज़ार थे और सबसे छोटी संख्या सैकड़ों (सौ) अथवा दहाइयों (दस) में थी।

इसी प्रकार के पाँच और प्रश्न बनाइए और उन्हें हल करने के लिए अपने मित्रों को दीजिए।
हम 4875 और 3542 की तुलना किस प्रकार करते हैं? यहाँ यह अधिक कठिन नहीं है।

इन दोनों संख्याओं में अंकों की संख्या समान है। ये दोनों हज़ारों में हैं। परंतु 4875 में हज़ार के स्थान पर अंक, 3542 के हज़ार के स्थान के अंक से बड़ा है। अतः 3542 से 4875 बड़ी है।

अब बताइए कि कौन सी संख्या बड़ी है; 4875 या 4542?
यहाँ भी दोनों संख्याओं में अंकों की संख्या समान (बराबर) है। साथ ही, दोनों में हज़ार के स्थान पर समान अंक हैं। अब हम क्या करते हैं? अब हम अगले अंक की ओर बढ़ते हैं, अर्थात् सौ के स्थान पर आने वाले अंकों को देखते हैं। 4875 में सौवें स्थान वाला अंक 4542 के सौवें स्थान वाले अंक से बड़ा है। अतः संख्या 4542 से संख्या 4875 बड़ी है।

यदि दोनों संख्याओं में सौ के स्थान वाले अंक भी समान होते, तो हम क्या करते?
4875 और 4889 की तुलना कीजिए।
4875 और 4879 की तुलना कीजिए।

प्रयास कीजिए

प्रत्येक समूह में सबसे बड़ी और सबसे छोटी संख्याएँ ज्ञात कीजिए:
(a) 4536, 4892, 4370, 4452
(b) 15623, 15073, 15189, 15800
(c) 25286, 25245, 25270, 25210
(d) 6895, 23787, 24569, 24659
इसी प्रकार के पाँच प्रश्न और बनाइए और हल करने के लिए अपने मित्रों को दीजिए।

1.2.1 आप कितनी संख्याएँ बना सकते हैं?

मान लीजिए हमारे पास अंक 7, 8, 3 और 5 हैं। हमें इन अंकों से चार अंकों वाली भिन्न-भिन्न ऐसी संख्याएँ बनाने को कहा जाता है कि एक संख्या में कोई भी अंक दोबारा न आए (अर्थात् किसी भी अंक की पुनरावृत्ति न हो)। इस प्रकार, संख्या 7835 तो बनाई जा सकती है, परंतु 7735 नहीं। इन 4 अंकों से जितनी संख्याएँ बना सकते हैं, बनाइए।

आपको सबसे बड़ी और सबसे छोटी संख्या कौन सी प्राप्त होती है? यहाँ सबसे बड़ी संख्या 8753 है और सबसे छोटी संख्या 3578 है। दोनों में अंकों के क्रम के बारे में सोचिए। क्या आप बता सकते हैं कि दिए गए अंकों से सबसे बड़ी संख्या किस प्रकार ज्ञात की जा सकती है? अपनी प्रक्रिया को लिखिए।

प्रयास कीजिए

प्रशन 1.
बिना पुनरावृत्ति किए, दिए हुए अंकों का प्रयोग करके चार अंकों की सबसे बड़ी और सबसे छोटी संख्याएँ बनाइए :
(a) 2, 8, 7, 4
(b) 9, 7, 4, 1
(c) 4, 7, 5, 0
(d) 1, 7, 6, 2
(e) 5, 4, 0,3
(संकेत : 0754 तीन अंकों की संख्या है।)

 

प्रशन 2.
किसी एक अंक का दो बार प्रयोग करके चार अंकों की सबसे बड़ी और सबसे छोटी संख्याएँ बनाइए :
(a) 3,8,7
(b) 9,0,5
(c) 0,4,9
(d) 8,5,1
(संकेत : प्रत्येक स्थिति में सोचिए कि आप किस अंक का दो बार प्रयोग करेंगे।)

प्रशन 3.
दिए हुए प्रतिबंधों के साथ, किन्हीं चार अंकों का प्रयोग करके, 4 अंकों की सबसे बड़ी और सबसे छोटी संख्याएँ बनाइए :
(a) अंक 7 सदैव इकाई के स्थान पर रहे।
सबसे बड़ी

9

8

6

7

सबसे छोटी

1

0

2

7

( ध्यान दीजिए, अंक 0 से संख्या प्रारंभ नहीं हो सकती। क्यों?)
(b) अंक 4 सदैव दहाई के स्थान पर रहे।

सबसे बड़ी

0

0

4

0

सबसे छोटी

0

0

4

0

(c) अंक 9 सदैव सौ के स्थान पर रहे।
सबसे बड़ी

0

0

9

0

सबसे छोटी

0

0

9

0

(d) अंक 1 सदैव हज़ार के स्थान पर रहे।
सबसे बड़ी

0

0

1

0

सबसे छोटी

0

0

1

0

प्रशन 4.
मान लीजिए, आप दो अंक 2 और 3 लेते हैं। इन अंकों को समान बार दोहराते हुए, चार अंकों की संख्याएँ बनाइए। कौन सी संख्या सबसे बड़ी है? कौन सी संख्या सबसे छोटी है? आप ऐसी कुल कितनी संख्याएँ बना सकते हैं?

उचित क्रम में खड़े होना :

Figure 1

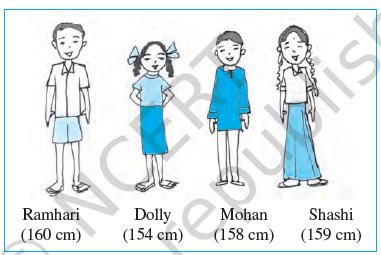
1. इनमें कौन सबसे लंबा है?
2. इनमें कौन सबसे छोटा है?
(a) क्या आप इन्हें इनकी लंबाइयों के बढ़ते हुए क्रम में खड़ा कर सकते हैं?
(b) क्या आप इन्हें इनकी लंबाइयों के घटते हुए क्रम में खड़ा कर सकते हैं?

क्या खरीदें?

Figure 2

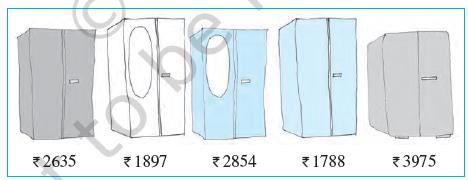
सोहन और रीता एक अलमारी खरीदने गए। वहाँ कई अलमारियाँ उपलब्ध थीं जिन पर उनके मूल्यों की पर्चियाँ लगी हुई थीं।
(a) क्या आप इनके मूल्यों को बढ़ते हुए क्रम में व्यवस्थित कर सकते हैं?
(b) क्या आप इनके मूल्यों को घटते हुए क्रम में व्यवस्थित कर सकते हैं?

प्रयास कीजिए

इसी प्रकार की पाँच और स्थितियों को सोचिए जहाँ आप तीन या अधिक राशियों की तुलना करते हैं।

आरोही क्रम ( Ascending order) :
आरोही या बढ़ते हुए क्रम का अर्थ है सबसे छोटे से प्रारंभ कर सबसे बड़े तक व्यवस्थित करना।

अवरोही क्रम (Descending order ) :
अवरोही क्रम या घटते हुए क्रम का अर्थ है सबसे बड़े से प्रारंभ कर सबसे छोटे तक व्यवस्थित करना।

प्रयास कीजिए

प्रशन 1.
निम्नलिखित संख्याओं को आरोही क्रम में व्यवस्थित कीजिए :
(a) 847, 9754, 8320, 571
(b) 9801, 25751, 36501, 38802

प्रशन 2.
निम्नलिखित संख्याओं को अवरोही क्रम में व्यवस्थित कीजिए :
(a) 5000, 7500, 85400, 7861
(b) 1971, 45321, 88715, 92547
आरोही/अवरोही क्रमों के ऐसे ही दस उदाहरण और बनाइए और उन्हें आरोही/अवरोही क्रम में व्यवस्थित कीजिए।

1.2.2 अंकों का स्थानांतरण

क्या आपने सोचा है कि यदि किसी संख्या के अंकों के स्थान परस्पर बदल दिए जाएँ तो क्या होगा?

सोचिए कि 182 क्या बन जाएगा। यह 821 जैसी बड़ी हो सकती है अथवा 128 जैसी छोटी हो सकती है । यही प्रक्रिया 391 के साथ करके देखिए।

अब आगे दिए हुए प्रश्नों पर ध्यान दीजिए। तीन भिन्न-भिन्न अंकों की कोई संख्या लीजिए और सौ के स्थान के अंक को इकाई के स्थान के अंक से बदलिए।

(a) क्या नयी संख्या पहली संख्या से बड़ी है?

(b) क्या नयी संख्या पहली संख्या से छोटी है?

इस प्रकार बनने वाली संख्याओं को आरोही और अवरोही दोनों क्रमों में लिखिए।

पहले

7

9

5

पहली और तीसरी टाइलों को परस्पर बदलने पर

बाद में

5

9

7

विभिन्न अंक लेकर यदि आप पहली और तीसरी टाइलों (अंकों) को परस्पर बदलते हैं, तो किस स्थिति में संख्या बड़ी हो जाती है? किस स्थिति में संख्या छोटी हो जाती है?

यह प्रक्रिया चार अंकों की कोई संख्या लेकर दोहराइए।

1.2.3 संख्या 10000 का प्रवेश

हम जानते हैं कि 99 से आगे दो अंकों वाली कोई भी संख्या नहीं है। 99 दो अंकों की सबसे बड़ी संख्या है। इसी प्रकार 999, तीन अंकों की सबसे बड़ी संख्या है और चार अंकों की सबसे बड़ी संख्या 9999 है। यदि हम 9999 में 1 जोड़ें, तो हमें क्या प्राप्त होगा?

इस प्रतिरूप को देखिए
9 + 1 = 10 =10 * 1
99 + 1 = 100 = 10 * 10
999 + 1 = 1000 =10 * 100

हम देखते हैं कि

एक अंक की सबसे बड़ी संख्या + 1 = दो अंकों की सबसे छोटी संख्या,
दो अंकों की सबसे बड़ी संख्या + 1 = तीन अंकों की सबसे छोटी संख्या,
तीन अंकों की सबसे बड़ी संख्या + 1 = चार अंकों की सबसे छोटी संख्या।

तब हम क्या यह नहीं सोच सकते कि चार अंकों की सबसे बड़ी संख्या में 1 जोड़ने पर, हमें पाँच अंकों की सबसे छोटी संख्या प्राप्त होगी,
अर्थात् 9999 + 1 = 10000 होगा।

इस प्रकार, 9999 से ठीक आगे आने वाली संख्या 10000 है। इसे दस हज़ार कहते हैं। साथ ही, हम सोच सकते हैं कि 10000 = 10 * 1000 होगा।

1.2.4 स्थानीय मान पर पुनर्दृष्ट

आप स्थानीय मान के बारे में बहुत पहले पढ़ चुके हैं तथा 78 जैसी दो अंकों की संख्या का प्रसारित रूप आपको अवश्य याद होगा। यह इस प्रकार है :

78 = 70 + 8
= 7 * 10 + 8

इसी प्रकार, आपको तीन अंकों की संख्या जैसे 278 का प्रसारित रूप भी याद होगा। यह इस प्रकार है :
278 = 200 + 70 + 8
= 2 * 100 + 7 * 10 +8 * 1

हम कहते हैं कि 8 इकाई के स्थान पर है, 7 दहाई के स्थान पर है और 2, सौ के स्थान पर है।

बाद में, हमने इसी अवधारणा को चार अंकों की संख्या के लिए भी लागू कर लिया था। उदाहरणार्थ, 5278 का प्रसारित रूप है :
5278 = 5000 + 200 + 70 + 8
= 5 * 1000 + 2 * 100 + 7 * 10 +8 *1

यहाँ, इकाई के स्थान पर 8 , दहाई के स्थान पर 7 , सौ के स्थान पर 2 और हज़ार के स्थान पर 5 है।

संख्या 10000 ज्ञात हो जाने पर, हम इस अवधारणा को और आगे लागू कर सकते हैं। हम पाँच अंकों की संख्या जैसे 45278 को इस प्रकार लिख सकते हैं :

45278 = 4 * 10000 + 5 * 1000 + 2 * 100 + 7 * ×10 + 8 * 1

यहाँ हम कहते हैं कि इकाई के स्थान पर 8 , दहाई के स्थान पर 7 , सौ के स्थान पर 2 , हज़ार के स्थान पर 5 और दस हज़ार के स्थान पर 4 है। इस संख्या को पैंतालीस हज़ार दो सौ अठहत्तर पढ़ा जाता है। क्या अब आप 5 अंकों की सबसे छोटी और सबसे बड़ी संख्याएँ लिख सकते हैं?

प्रयास कीजिए

 

संख्याओं को पढ़िए और जहाँ-जहाँ रिक्त स्थान हैं उनके नाम लिखिए और प्रसारित रूप में लिखिए :

संख्या	संख्या का नाम	प्रसारित रूप
20000	बीस हज़ार	2×10000
26000	छब्बीस हज़ार	2×10000+6×1000
38400	अड़तीस हज़ार चार सौ	3×10000+8×1000+4×100
65740	पैंसठ हज़ार सात सौ चालीस	6×10000+5×1000+7×100+4×10
89324	नवासी हज़ार तीन सौ चौबीस	8×10000+9×1000+3×100+2×10+4
50000	---	---
41000	---	---
47300	---	---
57630	---	---
29485	---	---
29085	---	---
20085	---	---
20005	---	---

पाँच अंकों वाली पाँच और संख्याएँ लिखिए,उन्हें पढ़िए और उनको प्रसारित रूप में लिखिए।

1.2.5 संख्या 100000 का प्रवेश

पाँच अंकों की सबसे बड़ी संख्या कौन सी है?
पाँच अंकों की सबसे बड़ी संख्या में 1 जोड़ने पर छः अंकों की सबसे छोटी संख्या प्राप्त होनी चाहिए। अर्थात्
99,999 +1 = 1,00,000
इस संख्या को एक लाख नाम दिया जाता है। एक लाख, 99,999 के ठीक आगे आने वाली संख्या है।
साथ ही, 10,000*10 = 1,00,000

अब हम 6 अंकों की संख्याएँ और उनके प्रसारित रूप लिख सकते हैं। जैसे :
2,46,853 = 2*1,00,000 + 4*10,000 + 6*1,000 + 8*100 + 5*10 +3*1

इस संख्या में,इकाई के स्थान पर 3,दहाई के स्थान पर 5,सौ के स्थान पर 8,हज़ार के स्थान पर 6,दस हज़ार के स्थान पर 4 और लाख के स्थान पर 2 है। इस संख्या का नाम दो लाख छियालीस हज़ार आठ सौ तिरपन है।

प्रयास कीजिए

संख्याओं को पढ़कर उन्हें रिक्त स्थानों में प्रसारित रूप में और उनके नाम लिखिये:

संख्या	संख्या का नाम	प्रसारित रूप
300,000	तीन लाख	3 × 100,000
350,000	तीन लाख पचास हजार	3 × 100,000 + 5 × 10,000
353,500	तीन लाख तिरपन हज़ार पांच सौ	3 × 100,000 + 5 × 10,000 + 3 × 1000 + 5 × 100
457,928	---	---
407,928	---	---
400,829	---	---
400,029	---	---

 

1.2.6 बड़ी संख्याएँ

यदि हम 6 अंकों की सबसे बड़ी संख्या में 1 जोड़ें, तो हमें 7 अंकों की सबसे छोटी संख्या प्राप्त होती है, जिसे दस लाख कहते हैं।
6 अंकों की सबसे बड़ी संख्या और 7 अंकों की सबसे छोटी संख्या लिखिए।
7 अंकों की सबसे बड़ी संख्या और 8 अंकों की सबसे छोटी संख्या लिखिए। 8 अंकों की सबसे छोटी संख्या एक करोड़ है।

प्रतिरूप को पूरा कीजिए :
9 + 1 = 10
99 + 1 = 100
999 + 1 = रिक्त स्थान
9,999 + 1 = रिक्त स्थान
99,999 + 1 = रिक्त स्थान
9,99,999 + 1 = रिक्त स्थान
99,99,999 + 1 = 1,00,00,000

याद रखिए :

1 सौ = 10 दहाइयाँ

1 हज़ार =10 सौ = 100 दहाइयाँ

1 लाख =100 हज़ार = 1000 सौ

1 करोड़ =100 लाख = 10,000 हज़ार

प्रयास कीजिए

1. 10-1 क्या है?
2. 100-1 क्या है?
3. 10,000-1 क्या है?
4. 1,00,000-1 क्या है?
5. 1,00,00,000-1 क्या है?
(संकेत : प्रतिरूप को पहचानिए)

अनेक विभिन्न स्थितियों में हमारे सम्मुख बड़ी संख्याएँ आती हैं। उदाहरणार्थ

आपकी कक्षा के बच्चों की संख्या दो अंकों की होगी,जबकि आपके स्कूल के कुल बच्चों की संख्या 3 या 4 अंकों की होगी। पास के शहर में रहने वाले लोगों की संख्या और अधिक बड़ी होगी।
क्या यह 5 या 6 या 7 अंकों की संख्या है? क्या आप अपने राज्य में रहने वाले लोगों की संख्या के बारे में जानते हैं?

इस संख्या में कितने अंक होंगे?

गेहूँ से भरी एक बोरी में दानों (grains) की संख्या क्या होगी? यह एक 5 अंकों की संख्या या 6 अंकों की संख्या या और बड़ी संख्या होगी?

प्रयास कीजिए

 

1. ऐसे पाँच उदाहरण दीजिए जहाँ गिनी जाने वाली वस्तुओं की संख्या 6 अंकों की संख्या से अधिक होगी।
2. 6 अंकों की सबसे बड़ी संख्या से प्रारंभ करते हुए, अवरोही क्रम में पिछली पाँच संख्याएँ लिखिए।
3. 8 अंकों की सबसे छोटी संख्या से प्रारंभ करते हुए, आरोही क्रम में अगली पाँच संख्याएँ लिखिए और उन्हें पढ़िए।

1.2.7 बड़ी संख्याएँ पढ़ने और लिखने में एक सहायता

निम्नलिखित संख्याओं को पढ़ने का प्रयत्न कीजिए :

(a) 279453
(b) 5035472
(c) 152700375
(d) 40350894

क्या आपको कुछ कठिनाई हुई?
आपको ऐसा करने में क्या कठिनाई हुई?

कभी-कभी बड़ी संख्याओं के पढ़ने और लिखने में कुछ सूचक (indicators) लगे होते हैं। शगुफ्ता भी सूचकों का प्रयोग करती है जो उसे बड़ी संख्याओं को पढ़ने और लिखने में सहायता करते हैं। उसके ये सूचक, संख्याओं को प्रसारित रूप में लिखने में भी सहायक होते हैं। उदाहरणार्थ, वह 257 में इकाई के स्थान, दहाई के स्थान और सौ के स्थान पर अंकों को ज्ञात करके उन्हें सारणी में O,T और H के नीचे निम्न प्रकार से लिखती है:

H	T	O	प्रसारित रूप
2	5	7	2 × 100+5 × 10 + 7 × 1

 

इसी प्रकार, 2902 के लिए वह प्राप्त करती है :

Th	H	T	O	प्रसारित रूप
2	9	0	2	2×1000+9×100+0×10+2×1

 

वह इस अवधारणा को लाखों तक की संख्याओं के लिए लागू करती है, जैसा कि नीचे दी हुई सारणी में देखा जा सकता है। (हम इन्हें शगुफ्ता के खाने या बॉक्स (Boxes) कहेंगे)। ध्यान से देखिए और रिक्त स्थानों पर छूटी हुई प्रविष्टियों को भरिए :

संख्या	TLa	La	TTh	Th	H	T	O	संख्या नाम	प्रसारित रूप
7,34,543	---	7	3	4	5	4	3	सात लाख चौंतीस हज़ार पाँच सौ तैंतालीस	---
32,75,829	3	2	7	5	8	2	9	---	3×10,00,000+2×1,00,000+7×10,000+5×1000+8×100+2×10+9×1

इसी प्रकार, हम करोड़ों तक की संख्याओं को सम्मिलित कर सकते हैं, जैसा कि नीचे दिखाया गया है :

संख्या	TCr	Cr	TLa	La	TTh	Th	H	T	O	संख्या नाम
2,57,34,543	---	2	5	7	3	4	5	4	3	---
65,32,75,829	6	5	3	2	7	5	8	2	9	पैंसठ करोड़ बत्तीस लाख पचहत्तर हज़ार आठ सौ उनतीस

आप संख्याओं को प्रसारित रूप में लिखने के लिए अन्य तालिकाओं का प्रारूप भी बना सकते हैं।

अल्प विरामों (commas) का प्रयोग

आपने ध्यान दिया होगा कि उपरोक्त तालिकाओं में बड़ी संख्याओं के लिखने में हमने अल्प विरामों का प्रयोग किया है। बड़ी संख्याओं को पढ़ने और लिखने में अल्प विराम हमारी बड़ी सहायता करते हैं। संख्यांकन की भारतीय पद्धति (Indian system of numeration ) में हम इकाई, दहाई, सौ (सैकड़ा), हज़ारों का प्रयोग करते हैं तथा आगे लाखों और करोड़ों का प्रयोग करते हैं। हज़ारों, लाखों और करोड़ों को प्रदर्शित करने के लिए अल्प विरामों का प्रयोग किया जाता है।

पहला अल्प विराम सौ के स्थान (दाएँ से चलते हुए तीसरे अंक) के बाद आता है और हज़ारों को प्रदर्शित करता है। दूसरा अल्प विराम अगले दो अंकों (दाएँ से पाँचवें अंक) के बाद आता है। यह दस हज़ार के स्थान के बाद आता है और लाखों को प्रदर्शित करता है। तीसरा अल्प विराम अन्य दो अंकों (दाएँ से सातवें अंक) के बाद आता है। यह दस लाख के स्थान के बाद आता है और करोड़ों को प्रदर्शित करता है।

उदाहरणार्थ
5,08,01,592
3,32,40,781
7,27,05,062

संख्याओं के नाम लिखते समय,हम अल्प विरामों का प्रयोग नहीं करते हैं।

ऊपर दी हुई संख्याओं को पढ़ने का प्रयत्न कीजिए। इसी रूप में पाँच और संख्याओं को लिखिए और फिर उन्हें पढ़िए।

अंतर्राष्ट्रीय संख्यांकन पद्धति

संख्यांकन की अंतर्राष्ट्रीय (International) पद्धति में,इकाई,दहाई,सौ,हज़ारों और आगे मिलियनों (millions) का प्रयोग किया जाता है। हज़ारों और मिलियनों को प्रदर्शित करने के लिए अल्प विरामों का प्रयोग किया जाता है। अल्प विराम दाएँ से प्रत्येक तीसरे अंक के बाद आता है। पहला अल्प विराम हज़ारों को प्रदर्शित करता है और दूसरा अल्प विराम मिलियनों को प्रदर्शित करता है।

उदाहरणार्थ
संख्या 50,801,592 को अंतर्राष्ट्रीय पद्धति में पचास मिलियन आठ सौ एक हज़ार पाँच सौ बानवे पढ़ा जाता है। भारतीय पद्धति में,यह पाँच करोड़ आठ लाख एक हज़ार पाँच सौ बानवे है।
कितने लाख से एक मिलियन बनता है?
कितने मिलियन से एक करोड़ बनता है?
तीन बड़ी संख्याओं को लीजिए। इन्हें भारतीय और अंतर्राष्ट्रीय दोनों संख्यांकन पद्धतियों में व्यक्त कीजिए।
इसमें आपकी रुचि हो सकती है:
सौ मिलियनों से बड़ी संख्याओं को व्यक्त करने के लिए,अंतर्राष्ट्रीय पद्धति में बिलियनों (Billions) का प्रयोग किया जाता है।
1 बिलियन =1000 मिलियन

क्या आप जानते हैं?

भारत की जनसंख्या में इस प्रकार वृद्धि हुई है :
1921-1931 के अंतराल में करीब 27 मिलियन;
1931-1941 के अंतराल में करीब 37 मिलियन;
1941-1951 के अंतराल में करीब 44 मिलियन;
1951-1961 के अंतराल में करीब 78 मिलियन;

1991-2001 के अंतराल में कितनी वृद्धि हुई। इस जानकारी को प्राप्त करने का प्रयत्न कीजिए। क्या आप जानते हैं कि इस समय भारत की जनसंख्या कितनी है?
पता करने का प्रयत्न कीजिए।

प्रयास कीजिए

1. इन संख्याओं को बक्सों का प्रयोग करते हुए लिखिए और फिर प्रसारित रूप में लिखिए :
(i) 475320
(ii) 9847215
(iii) 97645310
(iv) 30458094

(a) इनमें कौन-सी संख्या सबसे छोटी है?
(b) इनमें कौन-सी संख्या सबसे बड़ी है?
(c) इन संख्याओं को आरोही और अवरोही क्रमों में व्यवस्थित कीजिए।

2. निम्नलिखित संख्याओं को देखिए :
(i) 527864
(ii) 95432
(iii) 18950049
(iv) 70002509

(a) इन संख्याओं को बक्सों का प्रयोग करते हुए लिखिए और फिर अल्प विरामों का प्रयोग करते हुए लिखिए।
(b) इन संख्याओं को आरोही और अवरोही क्रमों में व्यवस्थित कीजिए।

3. ऐसी ही तीन और बड़ी संख्याएँ लेकर इस प्रक्रिया को दोहराइए।

क्या आप संख्यांक लिखने में मेरी सहायता कर सकते हैं?
एक संख्या के संख्यांक लिखने के लिए आप पुन: बक्सों का प्रयोग कर सकते हैं:
(a) बयालीस लाख सत्तर हज़ार आठ।
(b) दो करोड़ नब्बे लाख पचपन हज़ार आठ सौ।
(c) सात करोड़ साठ हज़ार पचपन।

प्रयास कीजिए

1. आपके पास 4,5,6,0,7 और 8 के अंक हैं। इनका प्रयोग करते हुए 6 अंकों की पाँच संख्याएँ बनाइए।
(a) पढ़ने में सरलता के लिए अल्प विराम लगाइए।
(b) इन्हें आरोही और अवरोही क्रमों में व्यवस्थित कीजिए।

2. अंकों 4,5,6,7,8 और 9 का प्रयोग कर 8 अंकों की कोई तीन संख्याएँ बनाइए। पढ़ने में सरलता के लिए, अल्प विरामों का प्रयोग कीजिए।

3. अंकों 3,0 और 4 का प्रयोग कर 6 अंकों की पाँच संख्याएँ बनाइए। अल्प विरामों का भी प्रयोग कीजिए।

प्रश्नावली 1.1

Q1. रिक्त स्थानों को भरिए :
(a) 1 लाख = --- दस हज़ार
(b) 1 मिलियन = --- सौ हज़ार
(c) 1 करोड़ = --- दस लाख
(d) 1 करोड़ = --- मिलियन
(e) 1 मिलियन = --- लाख

Q2. सही स्थानों पर अल्प विराम लगाते हुए, संख्यांकों को लिखिए :
(a) तिहत्तर लाख पचहत्तर हज़ार तीन सौ सात
(b) नौ करोड़ पाँच लाख इकतालीस
(c) सात करोड़ बावन लाख इक्कीस हज़ार तीन सौ दो
(d) अट्ठावन मिलियन चार सौ तेईस हज़ार दो सौ दो
(e) तेईस लाख तीस हज़ार दस

Q3. उपयुक्त स्थानों पर अल्प विराम लगाइए और संख्या नामों को भारतीय संख्यांकन पद्धति में लिखिए :
(a) 87595762
(b) 8546283
(c) 99900046
(d) 98432701

Q4. उपयुक्त स्थानों पर अल्प विराम लगाइए और संख्या नामों को अंतर्राष्ट्रीय संख्यांकन पद्धति में लिखिए :
(a) 78921092
(b) 7452283
(c) 99985102
(d) 48049831